Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
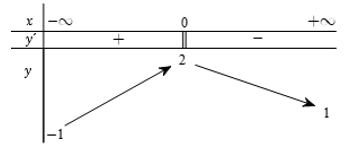
Khẳng định nào sau đây là đúng?
Trả lời bởi giáo viên
Dựa vào bảng biến thiên nhận thấy:
+) \(f\left( x \right) \le 2,\,\,\forall x \in \mathbb{R}\) và \(f\left( 0 \right) = 2\) nên GTLN của hàm số bằng \(2.\)
+) \(f\left( x \right) \ge - 1,{\rm{ }}\forall x \in \mathbb{R}\) và vì \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1\) nên không tồn tại \({x_0} \in \mathbb{R}\) sao cho \(f\left( {{x_0}} \right) = 1\), do đó hàm số không có GTNN.
Hướng dẫn giải:
Quan sát bảng biến thiên tìm GTLN và GTNN của hàm số, chú ý phải tồn tại \(x\) thuộc tập xác định để hàm số đạt GTLN, GTNN
Giải thích thêm:
Có thể giải thích cách khác: $y'$ đổi dấu qua $x = 0$ và tồn tại $y\left( 0 \right) = 2$ nên giá trị lớn nhất của hàm số bằng \(2\).