Cho hai hình vuông $ABCD,ABEF$ có chung cạnh $AB$ và nằm trong hai mặt phẳng khác nhau. Trên các đường chéo $AC$ và $BF$ ta lấy các điểm $M, N$ sao cho $AM = BN.$ Mặt phẳng $(P)$ chứa $MN$ và song song với $AB$ cắt $AD$ và $AF$ lần lượt tại $M’, N’.$ Khẳng định nào sau đây là đúng?
Trả lời bởi giáo viên
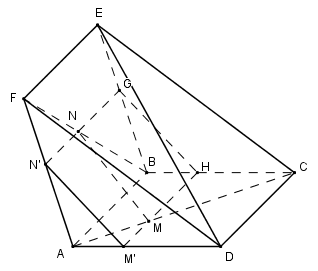
Trong (ABCD) qua M kẻ MM’ // AB \(\left( {M' \in AD} \right)\)
Trong (ABEF) qua N kẻ NN’ // AB \(\left( {N' \in AF} \right)\)
Ta có:
\(\left\{ \begin{array}{l}\dfrac{{AM'}}{{AD}} = \dfrac{{AM}}{{AC}}\\\dfrac{{AN'}}{{AF}} = \dfrac{{BN}}{{BF}}\\AM = BN;AC = BF\end{array} \right. \Rightarrow \dfrac{{AM'}}{{AD}} = \dfrac{{AN'}}{{AF}} \Rightarrow M'N'//DF\)
Lại có NN’ // AB // EF \( \Rightarrow \left( {MM'N'N} \right)//\left( {DEF} \right)\)
Mà \(MN \subset \left( {MM'N'N} \right) \Rightarrow MN//\left( {DEF} \right)\)
Hướng dẫn giải:
+) Trong (ABCD) qua M kẻ MM’ // AB \(\left( {M' \in AD} \right)\)
Trong (ABEF) qua N kẻ NN’ // AB \(\left( {N' \in AF} \right)\)
+) Dựa vào phương pháp chứng minh hai mặt phẳng song song: Hai đường thẳng cắt nhau trong mặt phẳng này lần lượt song song với hai đường thẳng trong mặt phẳng kia thì hai mặt phẳng đó song song
và tính chất: Nếu hai mặt phẳng song song thì mọi đường thẳng nằm trong mặt phẳng này song song với mặt phẳng kia.