Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
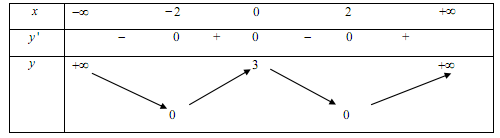
Khẳng định nào sau đây là khẳng định đúng?
Trả lời bởi giáo viên
A sai vì hàm số chỉ nghịch biến trên các khoảng $\left( { - \infty ; - 2} \right)$ và $\left( {0;2} \right)$
B sai vì hàm số đạt giá trị cực đại là $y = 3$ tại $x = 0$
C đúng vì từ bảng biến thiên ta thấy:
$\mathop {\min }\limits_R f\left( x \right) = 0 \Rightarrow f\left( x \right) \geqslant 0,\forall x \in R$
D sai vì hàm số chỉ đồng biến trên khoảng $\left( { - 2;0} \right)$ và $\left( {2; + \infty } \right)$
Hướng dẫn giải:
Quan sát bảng biến thiên và nhận xét các điểm cực đại, cực tiểu, giá trị cực đại, cực tiểu, khoảng đồng biến, nghịch biến của hàm số và rút ra kết luận.
Giải thích thêm:
Một số em có thể nhìn nhầm đáp án C $f(x) \ge 0$ thành $f'(x)\ge 0$ và nghĩ hàm số đồng biến trên $R$ và không chọn được đáp án.
Cần chú ý đọc kỹ các đáp án.