Đề thi thử THPTQG - Đề số 6

Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm $A\left( {0;0;1} \right)$, $B\left( { - 1; - 2;0} \right)$ và $C\left( {2;1; - 1} \right)$. Đường thẳng $\Delta$ đi qua trọng tâm $G$ của tam giác $ABC$ và vuông góc với mặt phẳng $\left( {ABC} \right)$ có phương trình là:

Công thức tính diện tích xung quanh hình nón có bán kính đáy $r$ và độ dài đường sinh $l$ là

Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$, $\widehat {ACB} = {60^0}$, cạnh $BC = a$, đường chéo $A'B$ tạo với mặt phẳng $\left( {ABC} \right)$ một góc ${30^0}$. Thể tích khối lăng trụ $ABC.A'B'C'$ là:

Trong các hàm số sau, hàm số nào đồng biến trên $R?$

Trong không gian với hệ tọa độ $Oxyz$, cho đường thẳng $d:\dfrac{x}{1} = \dfrac{{y - 1}}{2} = \dfrac{{z + 1}}{{ - 1}}$  và điểm $A\left( {5,4, - 2} \right)$. Phương trình mặt cầu đi qua điểm $A$ và có tâm là giao điểm của $d$ với mặt phẳng $(Oxy)$ là

Cho hàm số $f\left( x \right)$ có đạo hàm trên $R$. Nếu hàm số $f\left( x \right)$ nghịch biến trên $R$ thì:

Tính $F(x) = \int {x\cos x{\mkern 1mu} {\rm{d}}x}$ ta được kết quả

Trong không gian $Oxyz$, mặt phẳng $\left( {Oyz} \right)$ có phương trình là

Hàm số $F\left( x \right)$ được gọi là nguyên hàm của hàm số $f\left( x \right)$ nếu:

Chọn kết luận sai:

Cho hai số phức $z = \left( {2x + 3} \right) + \left( {3y - 1} \right)i$ và $z' = 3x + \left( {y + 1} \right)i$. Khi $z = z'$, chọn khẳng định đúng trong các khẳng định sau:

Một lớp có $8$ học sinh được bầu chọn vào 3 chức vụ khác nhau: lớp trưởng, lớp phó và bí thư (không được kiêm nhiệm). Số cách lựa chọn khác nhau sẽ là:

Cho cấp số cộng $\left( {{u_n}} \right)$ có số hạng đầu ${u_1} = 2$  và công sai $d = 5.$ Giá trị của ${u_4}$ bằng

Hàm số nào sao đây nghịch biến trên $\mathbb{R}$.

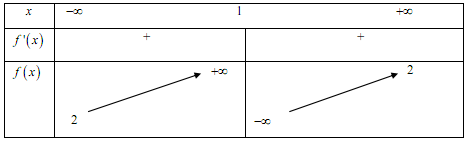
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?

Cho  $a > 0,a \ne 1$. Tìm mệnh đề đúng trong các mệnh đề sau:

Cho một mặt cầu bán kính bằng $1$. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?

Cho hàm số $y = f\left( x \right)$ đồng biến trên $\left( { - 3;7} \right)$ và xác định tại hai điểm $x =  - 3;x = 7$. Chọn kết luận đúng:

Trong không gian với hệ tọa độ $Oxyz,$ cho điểm $I\left( 3;4;-\,2 \right).$ Lập phương trình mặt cầu tâm $I$ và tiếp xúc với trục $Oz.$

Cho hàm số $y = f\left( x \right)$ có bảng biến thiên:

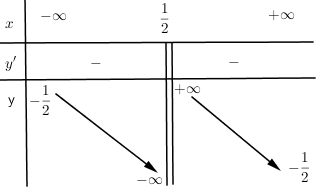
Khẳng định nào sau đây là đúng?

Đồ thị hàm số $y = {x^4} - {x^2} + 1$ và đồ thị của hàm số $y =  - {x^2}$ có tất cả bao nhiêu điểm chung?

Phương trình $\dfrac{1}{{{{\log }_2}x}} + \dfrac{1}{{{{\log }_3}x}} + ... + \dfrac{1}{{{{\log }_{2019}}x}} = 2$ có nghiệm thỏa mãn điều kiện nào dưới đây?

Có bao nhiêu số phức $z$ thỏa mãn $z - \bar z = {z^2}$?

Trong các mệnh đề sau, mệnh đề nào sai?

Cho mặt phẳng $\left( P \right):2x - z + 1 = 0$, tìm một véc tơ pháp tuyến của mặt phẳng $\left( P \right)$?

Tìm $m$ để hàm số $y = {x^3} - 3m{x^2} + 3\left( {2m - 1} \right)x + 1$ đồng biến trên $\mathbb{R}.$

Cho hàm số $y = \dfrac{{2mx + 1}}{{m - x}}.$ Giá trị lớn nhất của hàm số trên $\left[ {2;3} \right]$ bằng $\dfrac{{ - 1}}{3}$ khi m bằng:

Đồ thị hàm số $y = \dfrac{x}{{\sqrt {{x^2} - 1} }}$ có bao nhiêu đường tiệm cận ngang:

Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ như hình vẽ bên

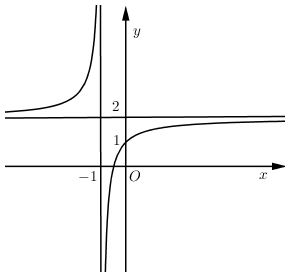
Chọn khẳng định đúng:

Cho số thực $x$ thỏa mãn ${\log _2}\left( {{{\log }_8}x} \right) = {\log _8}\left( {{{\log }_2}x} \right).$Tính giá trị của $P = {\left( {{{\log }_2}x} \right)^2}$

Cho ba số thực dương $a, b, c$ khác $1$. Đồ thị các hàm số $y = \log_{a} x, y=\log_{b} x, y= \log_{c} x$ được cho trong hình vẽ sau:

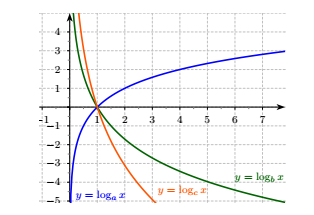
Mệnh đề nào dưới đây đúng?

Cho hàm số $f\left( x \right) = \dfrac{{{3^x}}}{{{7^{{x^2} - 4}}}}$. Hỏi khẳng định nào sau đây là sai?

Phát biểu nào sau đây là đúng?

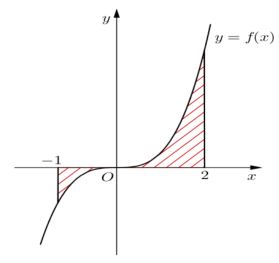
Gọi $S$ là diện tích hình phẳng $\left( H \right)$ giới hạn bởi các đường $y=f\left( x \right),~$trục hoành và hai đường thẳng $x =  - 1,x = 2$ (như hình vẽ). Đặt $a=\underset{-1}{\overset{0}{\mathop \int }}\,f\left( x \right)dx,~b=\underset{0}{\overset{2}{\mathop \int }}\,f\left( x \right)dx.$  Mệnh đề nào sau đây đúng?

Tìm phần ảo $b$ của số phức $w = 1 + \left( {1 + i} \right) + {\left( {1 + i} \right)^2} + {\left( {1 + i} \right)^3} + ... + {\left( {1 + i} \right)^{2018}}$.

Cho số phức $w$ và hai số thực $a,{\rm{ }}b.$ Biết rằng $w + i$ và $2w - 1$ là hai nghiệm của phương trình ${z^2} + az + b = 0.$ Tính tổng $S = a + b.$

Tập hợp các điểm trên mặt phẳng tọa độ $Oxy$ biểu diễn số phức $z$ thỏa mãn điều kiện: số phức $w = (z - i)(2 + i)$ là một số thuần ảo là:

Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$. Mặt phẳng $\left( {SAB} \right)$ và $\left( {SAD} \right)$ cùng vuông góc với mặt phẳng $\left( {ABCD} \right)$. Đường thẳng $SC$ tạo với đáy góc ${45^0}$. Gọi $M,N$ lần lượt là trung điểm của $AB$ và $AD$. Thể tích của khối chóp $S.MCDN$ là:

Cho hình lăng trụ xiên $ABC.A’B’C’$ có đáy $ABC$ là tam giác đều với tâm $O$. Hình chiếu của $C’$ trên $(ABC)$ là $O$. Tính thể tích của lăng trụ biết rằng khoảng cách từ $O$ đến $CC’$ là $a$ và 2 mặt bên $(ACC’A’)$ và $(BCC’B’)$ hợp với nhau góc ${90^0}$.

Cho tam giác $ABO$ vuông tại $O$, có góc $\widehat {BAO} = {30^0},AB = a$ . Quay tam giác $ABO$ quanh trục $AO$ ta được một hình nón có diện tích xung quanh bằng:

Cho hình chóp $S.ABCD$ có đáy là hình thang vuông $ABCD$ vuông tại $A$ và $D$, $AB = 2a,$ $AD = CD = a$. Cạnh bên $SA = a$ và vuông góc với mặt phẳng $\left( {ABCD} \right).$ Gọi $\varphi$ là góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$ . Mệnh đề nào sau đây đúng?

Cho hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $B$, $AD = a,$ $AB = 2a,$ $BC = 3a,$ $SA = 2a$, $H$ là trung điểm cạnh $AB$, $SH$ là đường cao của hình chóp $S.ABCD$. Tính khoảng cách từ điểm $A$ đến mặt phẳng $\left( {SCD} \right)$.

Cho số phức $z$ thỏa mãn $\left| {z - 2} \right| = 2$. Biết rằng tập hợp các điểm biểu diễn các số phức $w = \left( {1 - i} \right)z + i$ là một đường tròn. Tính bán kính $r$ của đường tròn đó

Trong không gian với hệ tọa độ Oxyz cho tứ diện ABCD có các đỉnh $A(1;2;1),B( - 2;1;3),C(2; - 1;1),D(0;3;1)$. Phương trình mặt phẳng (P) đi qua hai điểm A,B sao cho C,D khác phía so với (P) và khoảng cách từ C đến (P) bằng khoảng cách từ D đến (P) là:

Ông Bình đặt thợ làm một bể cá, nguyên liệu bằng kính trong suốt, không có nắp đậy dạng hình hộp chữ nhật có thể tích chứa được $220500\,\,{\rm{c}}{{\rm{m}}^{\rm{3}}}$ nước. Biết tỉ lệ giữa chiều cao và chiều rộng của bể bằng $3$. Xác định diện tích đáy của bể cá để tiết kiệm nguyên vật liệu nhất.

Một người lần đầu gửi vào ngân hàng $100$ triệu đồng với kì hạn $3$ tháng, lãi suất $2\%$ một quý theo hình thức lãi kép. Sau đúng 6 tháng, người đó gửi thêm $100$ triệu đồng với kì hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được sau 1 năm gửi thêm tiền gần nhất với kết quả nào sau đây?

Biết rằng phương trình ${\left[ {{{\log }_{\dfrac{1}{3}}}\left( {9x} \right)} \right]^2} + {\log _3}\dfrac{{{x^2}}}{{81}} - 7 = 0$ có hai nghiệm phân biệt ${x_1},{\rm{ }}{x_2}$. Tính $P = {x_1}{x_2}.$

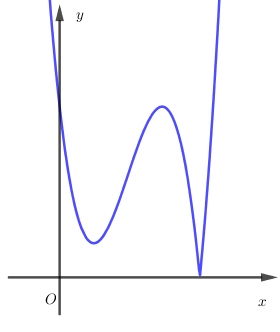
Cho hàm số $y = f\left( x \right)$ liên tục trên $R$ đồng thời hàm số $y = \left| {f\left( x \right)} \right|$ có đồ thị như hình vẽ bên, xác định số điểm cực trị của đồ thị hàm số $y = f\left( {\left| x \right|} \right)$.

Trong không gian Oxyz, cho điểm $E\left( {2;1;3} \right)$, mặt phẳng $\left( P \right):\,\,2x + 2y - z - 3 = 0$  và mặt cầu $\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 5} \right)^2} = 36$. Gọi $\Delta$ là đường thẳng đi qua E, nằm trong $\left( P \right)$ và cắt $\left( S \right)$ tại hai điểm có khoảng cách nhỏ nhất. Phương trình của $\Delta$ là:

Cho hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình bên. Đặt $g\left( x \right) = f\left( {\sqrt {{x^2} + x + 2} } \right)$. Chọn khẳng định đúng trong các khẳng định sau