Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \(a\). Mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Đường thẳng \(SC\) tạo với đáy góc \({45^0}\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AD\). Thể tích của khối chóp \(S.MCDN\) là:
Trả lời bởi giáo viên
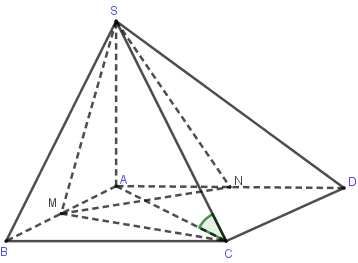
\(\left. \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \bot \left( {ABCD} \right)\\\left( {SAB} \right) \cap \left( {SAD} \right) = SA\end{array} \right\} \Rightarrow SA \bot \left( {ABCD} \right)\)
\( \Rightarrow AC\) là hình chiếu vuông góc của $SC$ trên \(\left( {ABCD} \right) \Rightarrow \widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA} = {45^0}\)
(vì \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A \Rightarrow \widehat {SCA} < {90^o}\))
\( \Rightarrow SA = AC = a\sqrt 2 \)
\(\begin{array}{l}{S_{ABCD}} = {a^2}\\{S_{AMN}} = \dfrac{1}{2}AM.AN = \dfrac{1}{2}\dfrac{a}{2}\dfrac{a}{2} = \dfrac{{{a^2}}}{8}\\{S_{BCM}} = \dfrac{1}{2}BM.BC = \dfrac{1}{2}\dfrac{a}{2}.a = \dfrac{{{a^2}}}{4}\\ \Rightarrow {S_{MCDN}} = {S_{ABCD}} - {S_{AMN}} - {S_{BCM}} = {a^2} - \dfrac{{{a^2}}}{8} - \dfrac{{{a^2}}}{4} = \dfrac{{5{a^2}}}{8}\\ \Rightarrow {V_{S.MCDN}} = \dfrac{1}{3}SA.{S_{MCDN}} = \dfrac{1}{3}a\sqrt 2 .\dfrac{{5{a^2}}}{8} = \dfrac{{5{a^3}\sqrt 2 }}{{24}}\end{array}\)
Hướng dẫn giải:
- Chứng minh \(SA \bot \left( {ABCD} \right)\) và tính \(SA\).
- Xác định góc giữa đường thẳng \(SC\) và mặt phẳng đáy, sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Tính diện tích đáy \(MCDN\).
- Tính thể tích khối chóp theo công thức \(V = \dfrac{1}{3}Sh\).

