Trong không gian Oxyz, cho điểm \(E\left( {2;1;3} \right)\), mặt phẳng \(\left( P \right):\,\,2x + 2y - z - 3 = 0\) và mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 5} \right)^2} = 36\). Gọi \(\Delta \) là đường thẳng đi qua E, nằm trong \(\left( P \right)\) và cắt \(\left( S \right)\) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của \(\Delta \) là:
Trả lời bởi giáo viên
Dễ thấy \(E \in \left( P \right)\) . Gọi I\(\left( {3;2;5} \right)\) là tâm khối cầu.
Đường thẳng qua I vuông góc với (P): \(\left\{ \begin{array}{l}x = 3 + 2t\\y = 2 + 2t\\z = 5 - t\end{array} \right.\,\,\left( d \right)\).
Gọi H là hình chiếu của I lên (P) \( \Rightarrow H \in \left( d \right) \Rightarrow H\left( {3 + 2t;2 + 2t;5 - t} \right)\)
Lại có \(H \in \left( P \right)\)
\(\begin{array}{l} \Rightarrow 2\left( {3 + 2t} \right) + 2\left( {2 + 2t} \right) - 5 + t - 3 = 0\\ \Leftrightarrow 6 + 4t + 4 + 4t - 5 + t - 3 = 0\\ \Leftrightarrow 9t + 2 = 0 \Leftrightarrow t = \dfrac{{ - 2}}{9} \Rightarrow H\left( {\dfrac{{23}}{9};\dfrac{{14}}{9};\dfrac{{47}}{9}} \right)\\ \Rightarrow \overrightarrow {EH} \left( {\dfrac{5}{9};\dfrac{5}{9};\dfrac{{20}}{9}} \right) = \dfrac{5}{9}\left( {1;\;1;\;4} \right)//\left( {1;1;4} \right) = \overrightarrow a \end{array}\)
Để đường thẳng \(\left( \Delta \right)\) cắt mặt cầu (S) tại 2 điểm sao cho chúng có khoảng cách nhỏ nhất thì đường thẳng \(\left( \Delta \right)\) đi qua E và vuông góc với \(HE\).
Ta có: \(\left\{ \begin{array}{l}\overrightarrow {{u_\Delta }} \bot \overrightarrow {{n_P}} \\\overrightarrow {{u_\Delta }} \bot \overrightarrow a \end{array} \right. \Rightarrow \overrightarrow {{u_\Delta }} = \left[ {\overrightarrow {{n_P}} ;\overrightarrow a } \right] = \left( {\left| {\begin{array}{*{20}{c}}\begin{array}{l}2\\1\end{array}&\begin{array}{l} - 1\\4\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l} - 1\\4\end{array}&\begin{array}{l}2\\1\end{array}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}\begin{array}{l}2\\1\end{array}&\begin{array}{l}2\\1\end{array}\end{array}} \right|} \right) = \left( {9; - 9;\;0} \right) = 9\left( {1; - 1;0} \right)\).
Vậy đường thẳng \(\left( \Delta \right)\) đi qua E và nhận \(\left( {1; - 1;0} \right)\) là 1 VTCP.
Vậy phương trình đường thẳng \(\left( \Delta \right):\,\,\left\{ \begin{array}{l}x = 2 + t\\y = 1 - t\\z = 3\end{array} \right.\)
Hướng dẫn giải:
+) Gọi I là tâm mặt cầu, xác định hình chiếu H của điểm I lên (P).
+) Để đường thẳng \(\left( \Delta \right)\) cắt mặt cầu (S) tại 2 điểm sao cho chúng có khoảng cách nhỏ nhất thì đường thẳng \(\left( \Delta \right)\) đi qua E và vuông góc với \(HE\).
Giải thích thêm:
Cách chứng minh \(\Delta \) là đường thẳng đi qua E và vuông góc HE:
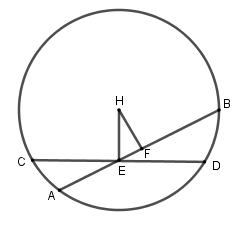
Mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn tâm H như hình vẽ.
Đường thẳng \(\Delta \) cắt (S) tại hai điểm cũng chính là giao điểm của \(\Delta \) với đường tròn trên.
Gọi AB, CD là hai dây cung đi qua E, trong đó \(CD \bot HE\) tại E.
F là hình chiếu của H lên AB.
Dễ thấy \(\Delta HEF\) vuông tại F nên HF < HE nên AB > CD (quan hệ giữa khoảng cách và dây trong đường tròn)
Vậy CD là dây cung đi qua E và có độ dài nhỏ nhất hay đường thẳng CD chính là đường thẳng \(\Delta \) cần tìm.

