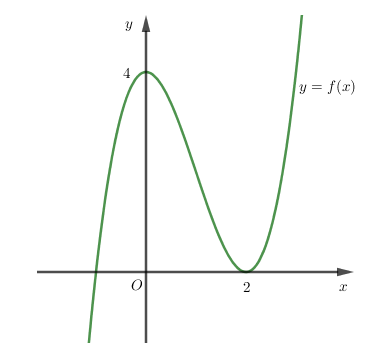
Cho hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình bên. Đặt $g\left( x \right) = f\left( {\sqrt {{x^2} + x + 2} } \right)$. Chọn khẳng định đúng trong các khẳng định sau
Trả lời bởi giáo viên
Hàm số $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$ ; $f'\left( x \right) = 3a{x^2} + 2bx + c$, có đồ thị như hình vẽ.
Do đó $x = 0 \Rightarrow d = 4$; $x = 2 \Rightarrow 8a + 4b + 2c + d = 0$; $f'\left( 2 \right) = 0 \Rightarrow 12a + 4b + c = 0$; $f'\left( 0 \right) = 0 \Rightarrow c = 0$.
Tìm được $a = 1;b = - 3;c = 0;d = 4$ và hàm số $y = {x^3} - 3{x^2} + 4$
Ta có $g\left( x \right) = f\left( {\sqrt {{x^2} + x + 2} } \right)$$ = {\left( {\sqrt {{x^2} + x + 2} } \right)^3} - 3\left( {{x^2} + x + 2} \right) + 4$ $ \Rightarrow g'\left( x \right) = \dfrac{3}{2}\left( {2x + 1} \right)\sqrt {{x^2} + x + 2} - 3\left( {2x + 1} \right) = 3\left( {2x + 1} \right)\left( {\dfrac{1}{2}\sqrt {{x^2} + x + 2} - 1} \right)$
$g'\left( x \right) = 0 \Rightarrow \left[ \begin{array}{l}x = - \dfrac{1}{2}\\x = 1\\x = - 2\end{array} \right.$
Bàng xét dấu của $g\left( x \right)$:
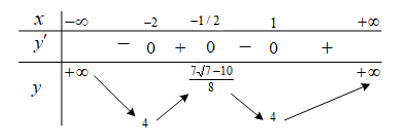
Vậy $g\left( x \right)$ nghịch biến trên khoảng $\left( {\dfrac{{ - 1}}{2};0} \right)$.
Hướng dẫn giải:
- Tìm hàm số \(y = f\left( x \right)\) dựa vào đồ thị đã cho.
- Tìm hàm số \(y = g\left( x \right)\) và xét hàm, tìm các khoảng đồng biến, nghịch biến của \(g\left( x \right)\)

