Cho hình chóp $S.ABCD$ có đáy là hình thang vuông $ABCD$ vuông tại $A$ và $D$, $AB = 2a,$ $AD = CD = a$. Cạnh bên $SA = a$ và vuông góc với mặt phẳng $\left( {ABCD} \right).$ Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$ . Mệnh đề nào sau đây đúng?
Trả lời bởi giáo viên
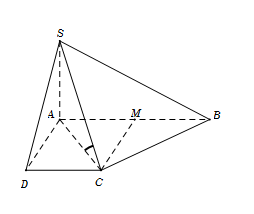
Gọi $M$ là trung điểm $AB$ $\, \Rightarrow ADCM$ là hình vuông.
Vì$\,CM = AD = a = \dfrac{{AB}}{2}$. Suy ra tam giác $ACB$ có trung tuyến bằng nửa cạnh đáy nên vuông tại $C$.
Ta có $\left\{ \begin{array}{l}BC \bot SA\\BC \bot AC\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot SC.$
Do đó :
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SC \bot BC\\\left( {ABCD} \right) \supset AC \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA}.$
Tam giác $SAC$ vuông tại $A$$ \Rightarrow \tan \varphi = \dfrac{{SA}}{{AC}} = \dfrac{{SA}}{{\sqrt {A{D^2} + C{D^2}} }} = \dfrac{a}{{a\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.$
Hướng dẫn giải:
Sử dụng phương pháp xác định góc giữa hai mặt phẳng và áp dụng các hệ thức lượng trong tam giác vuông

