Kết quả:
0/50
Thời gian làm bài: 00:00:00
Cho khối lăng trụ tứ giác đều có cạnh đáy bằng a, chiều cao 2a. Thể tích khối lăng trụ đã cho bằng
Cho số phức \(z = 6 + 7i\). Số phức liên hợp của z là:
Tập xác định của hàm số \(y = {\left( {x - 3} \right)^{ - 6}}\) là:
Họ nguyên hàm của hàm số \(y = {3^{x + 1}}\) là:
Số cách xếp 5 học sinh ngồi vào một dãy gồm 8 chiếc ghế bằng
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
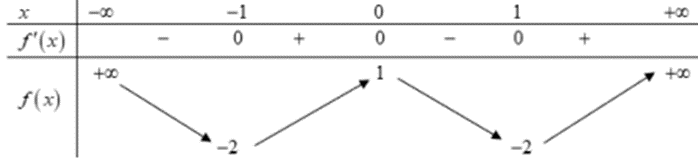
Số điểm cực trị của hàm số đã cho là:
Nếu \(\int\limits_1^2 {f\left( x \right)dx} = 3\) và \(\int\limits_2^5 {f\left( x \right)dx} = - 4\) thì \(\int\limits_1^5 {f\left( x \right)dx} \) bằng
Trong không gian Oxyz, cho hai điểm \(A\left( {1; - 3;2} \right)\) và \(B\left( {4;2; - 1} \right)\). Tọa độ của vectơ \(\overrightarrow {AB} \) là:
Tập nghiệm của bất phương trình \({4^x} \ge 2\) là:
Đồ thị hàm số \(y = {x^3} - 3{x^2} + 5x - 4\) đi qua điểm nào dưới đây?
Trên khoảng \(\left( {0; + \infty } \right)\), hàm số \(y = {\log _3}x\) có đạo hàm là:
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):\,\,2x + 5z - 3 = 0\). Một vectơ pháp tuyến của \(\left( P \right)\) có tọa độ là:
Thể tích khối chóp có diện tích đáy bằng 18 và chiều cao bằng 7 là:
Cho các số phức \({z_1} = 3 - 2i\) và \({z_2} = - 5 + 4i\), khi đó \({z_1} + {z_2}\) bằng
Tiệm cận ngang của đồ thị hàm số \(y = \dfrac{{2x - 1}}{{3x + 5}}\) là đường thẳng
Trong không gian Oxyz, tâm mặt cầu \(\left( S \right):\,\,{\left( {x - 3} \right)^2} + {y^2} + {\left( {z + 5} \right)^2} = 16\) có tọa độ là:
Thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\) được tính theo công thức nào dưới đây?
Nghiệm của phương trình \({\log _3}\left( {x + 5} \right) = 2\) là:
Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu đạo hàm như sau:
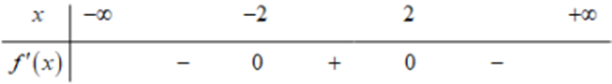
Hàm số đã cho nghịch biến trên khoảng nào dưới đây
Nếu \(\int\limits_3^4 {f\left( x \right)dx} = 5\) thì \(2\int\limits_3^4 {f\left( x \right)dx} \) bằng
Hàm số nào có đồ thị như đường cong trong hình dưới đây?
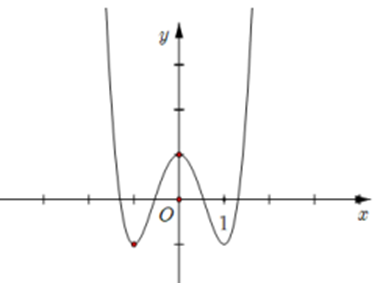
Trong không gian Oxyz, cho đường thẳng \(d:\,\,\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - t\\z = 3 + t\end{array} \right.\). Một vectơ chỉ phương của d có tọa độ là:
Diện tích mặt cầu có bán kính \(r\) bằng
Trong mặt phẳng tọa độ Oxy, số phức \(z = 2i\) được biểu diễn bởi điểm nào sau đây?
Với mọi số thực a dương, \({\log _3}\left( {3{a^2}} \right)\) bằng
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 5\) và công bội \(q = 6\). Giá trị của \({u_2}\) bằng
Giá trị cực đại của hàm số \(y = {x^3} - 3{x^2} + 2\) bằng
Tổng các nghiệm của phương trình \(\log _2^2x + {\log _2}x - 2 = 0\) bằng
Hàm số nào dưới đây nghịch biến trên \(\mathbb{R}\)?
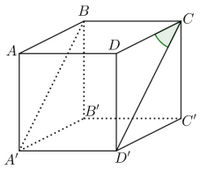
Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai đường thẳng \(BA'\) và \(CD\) bằng
Có 9 chiếc thẻ được đánh số từ 1 đến 9, người ta rút ngẫu nhiên hai thẻ khác nhau. Xác suất để rút được hai thẻ mà tích hai số được đánh trên thẻ là số chẵn bằng:
Trên đoạn \(\left[ {2;4} \right]\), hàm số \(y = {x^2} + \dfrac{2}{x}\) đạt giá trị lớn nhất tại điểm:
Trong không gian Oxyz, mặt phẳng đi qua điểm \(A\left( {1;2; - 3} \right)\) và vuông góc với đường thẳng \(d:\,\,\dfrac{{x - 3}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{{z - 2}}{3}\) có phương trình là:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\) và \(SA = 2a\) (tham khảo hình vẽ dưới)
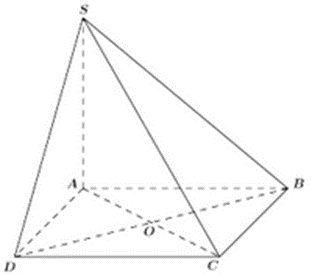
Khoảng cách từ điểm A đến mặt phẳng \(\left( {SBD} \right)\) bằng
Cho hàm số \(f\left( x \right) = 3{x^2} + \sin x\). Họ nguyên hàm của hàm số \(f\left( x \right)\) là:
Nếu \(\int\limits_0^3 {\left[ {4f\left( x \right) - 3{x^2}} \right]dx} = 5\) thì \(\int\limits_0^3 {f\left( x \right)dx} \) bằng:
Cho số phức \(z\) thỏa mãn \(\left( {1 + i} \right)\overline z = 1 - 3i\). Phần ảo của z bằng
Trong không gian Oxyz, cho mặt cầu \(\left( S \right):\,\,{\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 1} \right)^2} = 4\). Phương trình mặt phẳng nào dưới đây chứa trục hoành và tiếp xúc với (S)?
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật \(AB = 2,\,\,AD = 4\), SA vuông góc với mặt đáy, SB tạo với đáy góc \({60^0}\), điểm E thuộc cạnh SA và \(AE = \dfrac{{2\sqrt 3 }}{3}\). Mặt phẳng (BCE) cắt SD tại F. Thể tích khối đa diện ABCDEF bằng
Cho hàm số \(f\left( x \right) = {e^{\sqrt {{x^2} + 1} }}\left( {{e^x} - {e^{ - x}}} \right)\). Có bao nhiêu số nguyên dương m thỏa mãn bất phương trình \(f\left( {m - 7} \right) + f\left( {\dfrac{{12}}{{m + 1}}} \right) < 0\)?
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và thỏa mãn \(f\left( {{x^3} + 3x + 1} \right) = x + 3\). Tính \(\int\limits_1^5 {f\left( x \right)dx} \).
Có bao nhiêu số nguyên a để phương trình \({z^2} - \left( {a - 3} \right)z + {a^2} + a\) có 2 nghiệm \({z_1},\,\,{z_2}\) thỏa mãn \(\left| {{z_1} + {z_2}} \right| = \left| {{z_1} - {z_2}} \right|\)?
Tập hợp tất cả các giá trị thực của tham số m để hàm số \(y = \left| {{x^3} - 3{x^2} + m - 4} \right|\) có đúng 5 điểm cực trị là:
Cho hai hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + 3x\) và \(g\left( x \right) = m{x^3} + n{x^2} - x\), với \(a,b,c,m,n \in \mathbb{R}\). Biết hàm số \(y = f\left( x \right) - g\left( x \right)\) có 3 điểm cực trị là \( - 1,\,\,3\) và 4. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số \(y = f'\left( x \right)\) và \(y = g'\left( x \right)\) bằng:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
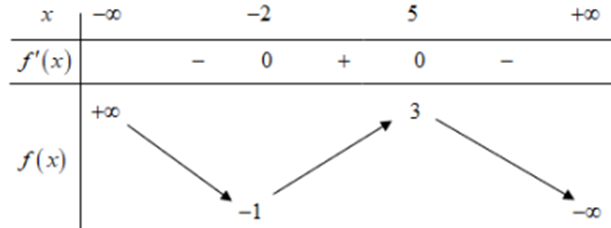
Số nghiệm thực của phương trình \(f'\left( {f\left( x \right)} \right) = 0\) là:
Cho hai số phức \({z_1},\,\,{z_2}\) thỏa mãn \(\left| {{z_1} + 3 + 2i} \right| = 1\) và \(\left| {{z_2} + 2 - i} \right| = 1\). Xét các số phức \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right)\) thỏa mãn \(2a - b = 0\). Khi đó biểu thức \(T = \left| {z - {z_1}} \right| + \left| {z - 2{z_2}} \right|\) đạt giá trị nhỏ nhất thì giá trị biểu thức \(P = {a^2} + {b^2}\) bằng:
Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e\,\,\left( {a \ne 0} \right)\) có đồ thị \(\left( C \right)\). Biết rằng \(\left( C \right)\) cắt trục hoành tại bốn điểm phân biệt là \(A\left( {{x_1};0} \right),\,\,B\left( {{x_2};0} \right)\), \(C\left( {{x_3};0} \right),\,\,D\left( {{x_4};0} \right)\), với \({x_1},{x_2},{x_3},{x_4}\) theo thứ tự lập thành cấp số cộng và hai tiếp tuyến của \(\left( C \right)\) tại A, B vuông góc với nhau. Khi đó, giá trị của biểu thức \(P = {\left[ {f'\left( {{x_3}} \right) + f'\left( {{x_4}} \right)} \right]^{2022}}\) bằng
Một đề thi trắc nghiệm gồm 50 câu hỏi độc lập. Mỗi câu hỏi có 4 đáp án trả lời, trong đó chỉ có một đáp án đúng. Mỗi câu trả lời đúng được 0,2 điểm, câu trả lời sai được 0 điểm. Học sinh A làm bài bằng cách chọn ngẫu nhiên câu trả lời cho tất cả 50 câu hỏi. Biết xác suất làm đúng k câu hỏi của học sinh Á đạt giá trị lớn nhất, khi đó giá trị k bằng
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây:
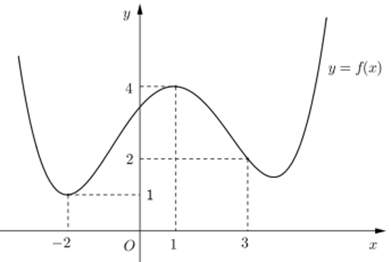
Có bao nhiêu giá trị nguyên của tham số m không vượt quá 2022 để bất phương trình \(\dfrac{m}{{f\left( x \right)}} - \sqrt {mf\left( x \right)} - 1 \ge \dfrac{3}{4}{f^2}\left( x \right)\) đúng với mọi \(x \in \left[ { - 2;3} \right]\)?
Trong không gian Oxyz, cho mặt phẳng \(\left( P \right):\,\,mx - 3y - \left( {2m - 3} \right)z - 9 = 0\) (m là tham số thực) và mặt cầu \(\left( S \right):\,\,{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {z^2} = 16\). Biết rằng (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất, khi đó khoảng cách từ điểm \(A\left( { - 1;2;3} \right)\) đến \(\left( P \right)\) bằng

