Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây:

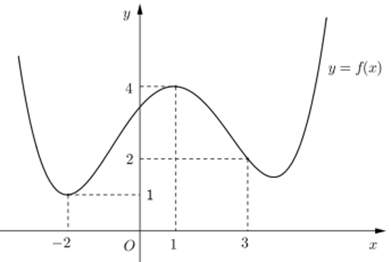
Có bao nhiêu giá trị nguyên của tham số m không vượt quá 2022 để bất phương trình \(\dfrac{m}{{f\left( x \right)}} - \sqrt {mf\left( x \right)}  - 1 \ge \dfrac{3}{4}{f^2}\left( x \right)\) đúng với mọi \(x \in \left[ { - 2;3} \right]\)?

Điều kiện: \(mf\left( x \right) \ge 0\).

Dựa vào đồ thị ta thấy: Với \(x \in \left[ { - 2;3} \right]\) thì \(f\left( x \right) \ge 0\) \( \Rightarrow m \ge 0\).

Ta có:

\(\begin{array}{l}\,\,\,\,\,\dfrac{m}{{f\left( x \right)}} - \sqrt {mf\left( x \right)}  - 1 \ge \dfrac{3}{4}{f^2}\left( x \right)\\ \Leftrightarrow \dfrac{m}{{f\left( x \right)}} - \sqrt {mf\left( x \right)}  + \dfrac{{{f^2}\left( x \right)}}{4} \ge {f^2}\left( x \right) + 1\\ \Leftrightarrow {\left( {\sqrt {\dfrac{m}{{f\left( x \right)}}}  - \dfrac{{f\left( x \right)}}{2}} \right)^2} \ge {f^2}\left( x \right) + 1\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt {\dfrac{m}{{f\left( x \right)}}}  - \dfrac{{f\left( x \right)}}{2} \ge \sqrt {{f^2}\left( x \right) + 1} \\\sqrt {\dfrac{m}{{f\left( x \right)}}}  - \dfrac{{f\left( x \right)}}{2} \le  - \sqrt {{f^2}\left( x \right) + 1} \end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}\sqrt m  \ge \sqrt {\left[ {{f^2}\left( x \right) + 1} \right]f\left( x \right)}  + \dfrac{1}{2}f\left( x \right)\sqrt {f\left( x \right)} \\\sqrt m  \le  - \sqrt {\left[ {{f^2}\left( x \right) + 1} \right]f\left( x \right)}  + \dfrac{1}{2}f\left( x \right)\sqrt {f\left( x \right)} \end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}\sqrt m  \ge \mathop {\max }\limits_{\left[ { - 2;3} \right]} \left\{ {\sqrt {\left[ {{f^2}\left( x \right) + 1} \right]f\left( x \right)}  + \dfrac{1}{2}f\left( x \right)\sqrt {f\left( x \right)} } \right\}\\\sqrt m  \le \mathop {\min }\limits_{\left[ { - 2;3} \right]} \left\{ { - \sqrt {\left[ {{f^2}\left( x \right) + 1} \right]f\left( x \right)}  + \dfrac{1}{2}f\left( x \right)\sqrt {f\left( x \right)} } \right\}\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\sqrt m  \ge 4 + 2\sqrt {17} \\\sqrt m  \le 4 - 2\sqrt {17} \end{array} \right.\end{array}\)

\( \Rightarrow m \ge {\left( {4 + 2\sqrt {17} } \right)^2} \approx 149,96\).

Kết hợp điều kiện đề bài có $2022-150+1=1873$

\( \Rightarrow \) Có 1873 giá trị m thỏa mãn.