Cho hai số phức \({z_1},\,\,{z_2}\) thỏa mãn \(\left| {{z_1} + 3 + 2i} \right| = 1\) và \(\left| {{z_2} + 2 - i} \right| = 1\). Xét các số phức \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right)\) thỏa mãn \(2a - b = 0\). Khi đó biểu thức \(T = \left| {z - {z_1}} \right| + \left| {z - 2{z_2}} \right|\) đạt giá trị nhỏ nhất thì giá trị biểu thức \(P = {a^2} + {b^2}\) bằng:

Gọi \({M_1},\,\,{M_2},\,\,M\) lần lượt là các điểm biểu diễn số phức \({z_1},\,\,2{z_2},\,\,z\).

Ta có:

+) \(\left| {{z_1} + 3 + 2i} \right| = 1 \Leftrightarrow \left| {{z_1} - \left( { - 3 - 2i} \right)} \right| = 1\).

\( \Rightarrow \) Tập hợp các điểm \({M_1}\) là đường tròn \(\left( {{C_1}} \right)\) tâm \({I_1}\left( { - 3; - 2} \right)\), bán kính \({R_1} = 1\).

+) \(\left| {{z_2} + 2 - i} \right| = 1 \Leftrightarrow \left| {2{z_2} - \left( { - 4 + 2i} \right)} \right| = 2\)

\( \Rightarrow \) Tập hợp các điểm \({M_2}\) là đường tròn \(\left( {{C_2}} \right)\) tâm \({I_2}\left( { - 4;2} \right)\), bán kính \({R_2} = 2\).

+) số phức \(z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right)\) thỏa mãn \(2a - b = 0\)

\( \Rightarrow \) Tập hợp các điểm \(M\) là đường thẳng \(d:\,\,2x - y = 0\).

Khi đó ta có: \(T = \left| {z - {z_1}} \right| + \left| {z - 2{z_2}} \right| = M{M_1} + M{M_2}\).

Gọi \(\left( {{C_3}} \right)\) đối xứng \(\left( {{C_1}} \right)\) qua d \( \Rightarrow \left( {{C_3}} \right)\) có tâm \({I_3}\left( {\dfrac{1}{5};\dfrac{{ - 18}}{5}} \right)\), bán kính \({R_3} = 1\).

Gọi \({M_3}\) đối xứng \({M_1}\) qua \(d\) \({M_3} \in \left( {{C_3}} \right)\).

Khi đó ta có: \(M{M_1} + M{M_2} = M{M_3} + M{M_2}\).

Gọi A, B lần lượt là giao điểm của \({I_2}{I_3}\) với \(\left( {{C_2}} \right),\,\,\left( {{C_3}} \right)\).

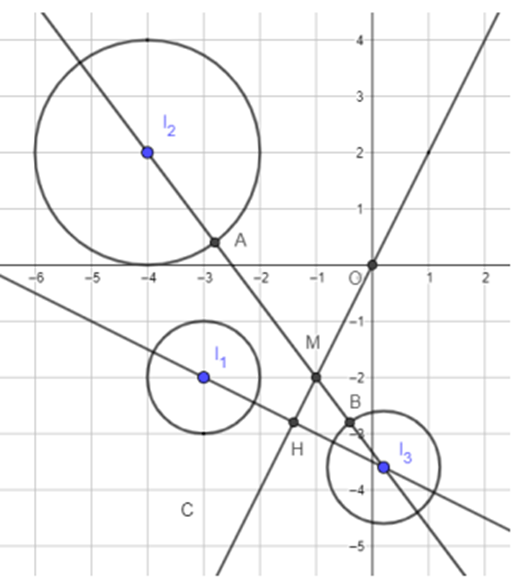
Ta có: \(M{M_2} + M{M_3} \ge AB\). Dấu “=” xảy ra khi \({M_1} \equiv A,\,\,{M_3} \equiv B\).

Khi đó \({P_{\min }} = AB = {I_2}{I_3} - 3 \)\(= \sqrt {{{\left( {\dfrac{1}{5} + 4} \right)}^2} + {{\left( { - \dfrac{{18}}{5} - 2} \right)}^2}}  - 3 = 4\).

Khi đó \(M = {I_2}{I_3} \cap d \Rightarrow M\left( { - 1; - 2} \right)\).

Vậy \(a =  - 1,\,\,b =  - 2\) nên \({a^2} + {b^2} = 5\).