Trả lời bởi giáo viên
Đáp án đúng: b
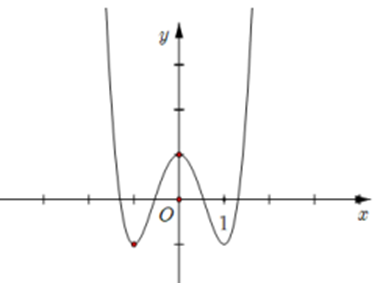
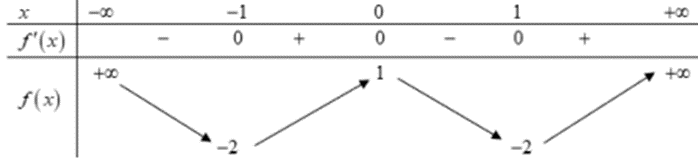
Hàm số đã cho là hàm bậc bốn trùng phương y=ax4+bx2+c.
Vì lim nên a > 0. Loại đáp án C.
Đồ thị cắt trục tung tại điểm có tung độ dương nên loại đáp án A.
Hàm số có 3 điểm cực trị nên ab < 0. Mà a > 0 \Rightarrow b < 0. Loại đáp án D.
Hướng dẫn giải:
Hàm số đã cho là hàm bậc bốn trùng phương y = a{x^4} + b{x^2} + c.
- Dựa vào \mathop {\lim }\limits_{x \to + \infty } y xác định dấu của a.
- Dựa vào giao điểm của đồ thị với trục tung xác định dấu của d.
- Dựa vào số điểm cực trị xác định dấu của b.
+ Nếu hàm số có 3 điểm cực trị thì ab < 0.
+ Nếu hàm số có 1 điểm cực trị thì ab \ge 0.