Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\) và \(SA = 2a\) (tham khảo hình vẽ dưới)

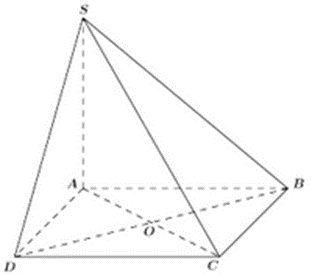
Khoảng cách từ điểm A đến mặt phẳng \(\left( {SBD} \right)\) bằng

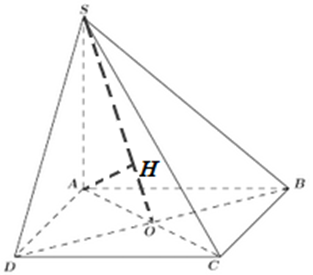
Ta có: \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\).

Trong \(\left( {SAC} \right)\) kẻ \(AH \bot SO\,\,\left( {H \in SO} \right)\) ta có: \(\left\{ \begin{array}{l}AH \bot SO\\AH \bot BD\end{array} \right. \Rightarrow AH \bot \left( {SBD} \right)\)\( \Rightarrow d\left( {A,\left( {SBD} \right)} \right) = AH\).

Vì ABCD là hình vuông cạnh a nên \(AO = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\).

Xét tam giác vuông SAO có: \(AH = \dfrac{{SA.AO}}{{\sqrt {S{A^2} + A{O^2}} }} = \dfrac{{2a.\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {4{a^2} + \dfrac{{{a^2}}}{2}} }} \)\(= \dfrac{{2a}}{3}\).

Vậy \(d\left( {A,\left( {SBD} \right)} \right) = \dfrac{{2a}}{3}\).