Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật \(AB = 2,\,\,AD = 4\), SA vuông góc với mặt đáy, SB tạo với đáy góc \({60^0}\), điểm E thuộc cạnh SA và \(AE = \dfrac{{2\sqrt 3 }}{3}\). Mặt phẳng (BCE) cắt SD tại F. Thể tích khối đa diện ABCDEF bằng

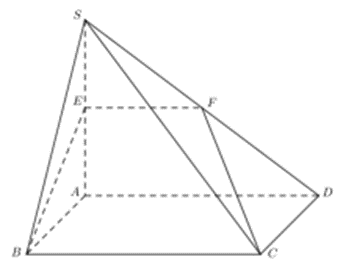
Xét \(\left( {BCE} \right)\) và \(\left( {SAD} \right)\) có: E chung, BC // AD

\( \Rightarrow \left( {BCE} \right) \cap \left( {SAD} \right) = EF//AD//BC\).

Ta có: \(SA \bot \left( {ABCD} \right) \Rightarrow \widehat{ \left( {SB,\left( {ABCD} \right)} \right)} \)\(= \widehat{ \left( {SB,AB} \right)} = \widehat{ SBA }= {60^0}\).

Xét tam giác SAB có: \(SA = AB.\tan {60^0} = 2\sqrt 3 \) \( \Rightarrow SE = SA - AE = 2\sqrt 3  - \dfrac{{2\sqrt 3 }}{3} = \dfrac{{4\sqrt 3 }}{3}\).

Vì EF // AD nên ta có: \(\dfrac{{SE}}{{SA}} = \dfrac{{SF}}{{SD}} = \dfrac{{4\sqrt 3 }}{3}:2\sqrt 3  = \dfrac{2}{3}\).

Ta có:

\(\begin{array}{l}\dfrac{{{V_{S.EBC}}}}{{{V_{S.ABC}}}} = \dfrac{{SE}}{{SA}} = \dfrac{2}{3} \\\Rightarrow {V_{S.EBC}} = \dfrac{2}{3}{V_{S.ABC}} = \dfrac{1}{3}{V_{S.ABCD}}\\\dfrac{{{V_{S.ECF}}}}{{{V_{S.ACD}}}} = \dfrac{{SE}}{{SA}}.\dfrac{{SF}}{{SD}} = \dfrac{4}{9}\\ \Rightarrow {V_{S.ECF}} = \dfrac{4}{9}{V_{S.ACD}} = \dfrac{2}{9}{V_{S.ABCD}}\\ \Rightarrow {V_{S.EBCF}} = {V_{S.EBC}} + {V_{S.ECF}} = \dfrac{5}{9}{V_{S.ABCD}}\end{array}\)

Mà \({V_{S.ABCD}} = \dfrac{1}{3}SA.{S_{ABCD}} = \dfrac{1}{3}SA.AB.AD \)\(= \dfrac{1}{3}.2\sqrt 3 .2.4 = \dfrac{{16\sqrt 3 }}{3}\).

\( \Rightarrow {V_{S.EBCF}} = \dfrac{5}{9}{V_{S.ABCD}} \)\(= \dfrac{{80\sqrt 3 }}{{27}}\).

Vậy \({V_{ABCDEF}} = {V_{S.ABCD}} - {V_{S.EBCF}} \)\(= \dfrac{{64\sqrt 3 }}{{27}}\).