Câu hỏi:
1 năm trước
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
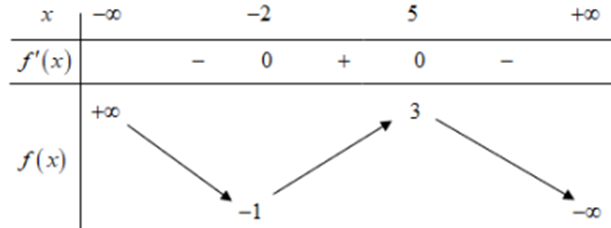
Số nghiệm thực của phương trình \(f'\left( {f\left( x \right)} \right) = 0\) là:
Trả lời bởi giáo viên
Đáp án đúng: b
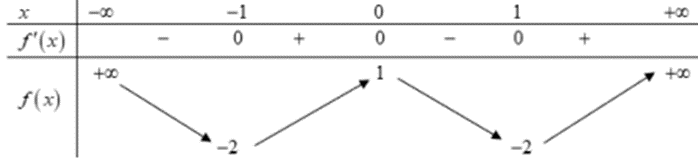
Dựa vào BBT ta thấy \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 5\end{array} \right.\).
Do đó \(f'\left( {f\left( x \right)} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = - 2\,\,\left( 1 \right)\\f\left( x \right) = 5\,\,\,\,\,\left( 2 \right)\end{array} \right.\).
Dựa vào BBT ta thấy phương trình (1) có 1 nghiệm, phương trình 2 có 1 nghiệm.
Vậy phương trình \(f'\left( {f\left( x \right)} \right) = 0\) có 2 nghiệm phân biệt.
Hướng dẫn giải:
Sử dụng tương giao đồ thị hàm số.