Cho hàm số $y = f\left( x \right)$ liên tục trên $R$ đồng thời hàm số $y = \left| {f\left( x \right)} \right|$ có đồ thị như hình vẽ bên, xác định số điểm cực trị của đồ thị hàm số $y = f\left( {\left| x \right|} \right)$.
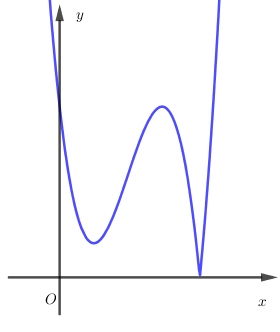
Trả lời bởi giáo viên
Từ hình vẽ ta có đồ thị hàm số $y = f\left( x \right)$ là một trong hai đồ thị dưới đây:
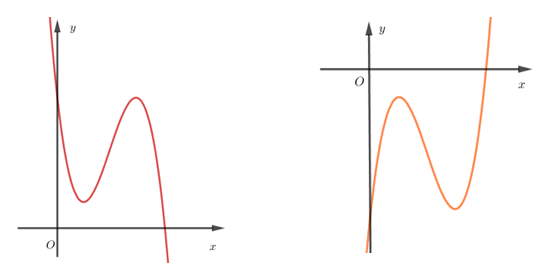
Từ hai đồ thị trên ta dựng được đồ thị $y = f\left( {\left| x \right|} \right)$ là một trong đồ thị dưới đây:
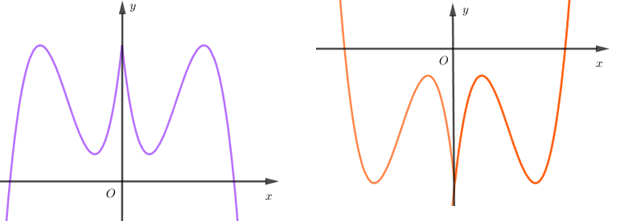
Từ hai đồ thị ở trên ta thấy: Ở cả hai trường hợp thì hàm số $y = f\left( {\left| x \right|} \right)$ đều có $5$ điểm cực trị.
Hướng dẫn giải:
- Dựng đồ thị hàm số $y = f\left( x \right)$ từ đồ thị hàm số $y = \left| {f\left( x \right)} \right|$
- Dựng đồ thị hàm số $y = f\left( {\left| x \right|} \right)$ có được từ đồ thị hàm số $y=f\left( x \right)$
Giải thích thêm:
Một số em khi quan sát đồ thị hàm số $y=f(|x|)$ sẽ đếm nhầm thêm hai điểm giao của đồ thị hàm số với trục hoành dẫn đến nghĩ rằng có $7$ điểm cực trị và không chọn được đáp án.

