Câu hỏi:
2 năm trước
Trong không gian \(Oxyz\), cho điểm \(S\left( { - 2;1; - 2} \right)\) nằm trên mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} = 9\). Từ điểm \(S\) kẻ ba dây cung \(SA,SB,SC\) với mặt cầu \(\left( S \right)\) có độ dài bằng nhau và đôi một tạo với nhau góc \({60^0}\). Dây cung \(AB\) có độ dài bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
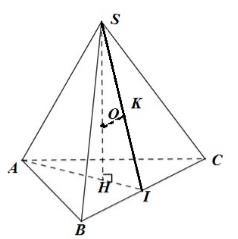
Xét tứ diện SABC có: \(SA = SB = SC\), \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA} = {60^0}\)\( \Rightarrow SABC\) là tứ diện đều.
Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} = 9\) có tâm O, bán kính \(R = 3\), ngoại tiếp khối tứ diện SABC \( \Rightarrow OS = OA = OB = OC = 3\)
Giả sử độ dài dây AB là a \( \Rightarrow \,SI = AI = \dfrac{{a\sqrt 3 }}{2}\)\( \Rightarrow \,AH = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
\( \Rightarrow SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{a^2} - \dfrac{1}{3}{a^2}} = \sqrt {\dfrac{2}{3}} a\)
\( \Rightarrow R = \dfrac{{{a^2}}}{{2\sqrt {\dfrac{2}{3}} a}} = \dfrac{{\sqrt 6 a}}{4} \Rightarrow \dfrac{{\sqrt 6 a}}{4} = 3 \Leftrightarrow a = 2\sqrt 6 \).
Hướng dẫn giải:
Gọi h là chiều cao của hình chóp, a là độ dài cạnh bên của hình chóp. Ta có: \(R = \dfrac{{{a^2}}}{{2h}}\).
Câu hỏi khác
- Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 4 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 1 Toán 12 có lời giải chi tiết
- Đề tập huấn thi THPTQG Sở Giáo Dục và Đào Tạo Bắc Ninh 2019 Toán 12 có lời giải chi tiết
