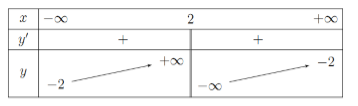
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) và bảng xét dấu của đạo hàm như hình vẽ sau

Có bao nhiêu số nguyên \(m \in \left( {0;2020} \right)\) để hàm số \(g\left( x \right) = f\left( {{x^2} - x + m} \right)\) nghịch biến trên khoảng \(\left( { - 1;0} \right)\)?
Trả lời bởi giáo viên
\(g\left( x \right) = f\left( {{x^2} - x + m} \right) \)
\(\Rightarrow g'\left( x \right) = \left( {2x - 1} \right).f'\left( {{x^2} - x + m} \right)\)
Với \(x \in \left( { - 1;0} \right)\) thì \(2x - 1 < 0\).
Do đó, để \(g\left( x \right) = f\left( {{x^2} - x + m} \right)\) nghịch biến trên khoảng \(\left( { - 1;0} \right)\) thì
\(\begin{array}{l}g'\left( x \right) \le 0,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow \left( {2x - 1} \right)f'\left( {{x^2} - x + m} \right) \le 0,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow f'\left( {{x^2} - x + m} \right) \ge 0,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - x + m \le 1\\{x^2} - x + m \ge 4\end{array} \right.,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} - x \le 1 - m\\{x^2} - x \ge 4 - m\end{array} \right.,\forall x \in \left( { - 1;0} \right)\end{array}\)
Xét hàm \(h\left( x \right) = {x^2} - x\) trong \(\left( { - 1;0} \right)\) ta thấy:
\(h'\left( x \right) = 2x - 1 < 0,\forall x \in \left( { - 1;0} \right)\) nên hàm số nghịch biến trong \(\left( { - 1;0} \right)\)
\(\begin{array}{l} \Rightarrow h\left( { - 1} \right) > h\left( x \right) > h\left( 0 \right)\\ \Leftrightarrow 2 > h\left( x \right) > 0 \Leftrightarrow 0 < h\left( x \right) < 2\end{array}\)
Do đó
\(\begin{array}{l}\left[ \begin{array}{l}h\left( x \right) \le 1 - m\\h\left( x \right) \ge 4 - m\end{array} \right.,\forall x \in \left( { - 1;0} \right)\\ \Leftrightarrow \left[ \begin{array}{l}
1 - m \ge \mathop {\max }\limits_{\left[ { - 1;0} \right]} h\left( x \right)\\
4 - m \le \mathop {\min }\limits_{\left[ { - 1;0} \right]} h\left( x \right)
\end{array} \right.\\\Leftrightarrow \left[ \begin{array}{l}1 - m \ge 2\\4 - m \le 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \le - 1\\m \ge 4\end{array} \right.\end{array}\)
Mà \(m \in \left( {0;2020} \right),\,\,\,\,m \in \mathbb{Z} \Rightarrow m \in \left\{ {4;5;6;...;2019} \right\}\): có 2016 giá trị.
Hướng dẫn giải:
+) Tính \(g'\left( x \right)\).
+) Tìm điều kiện để \(g'\left( x \right) \le 0\,\,\forall x \in \left( { - 1;0} \right)\).