Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), góc giữa mặt bên và mặt đáy bằng \({60^0}\). Gọi O là giao điểm của AC và BD. Tính khoảng cách từ O đến mặt phẳng \(\left( {SAB} \right)\).
Trả lời bởi giáo viên
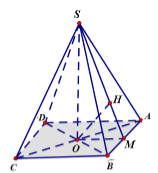
Gọi M là trung điểm của AB, dựng \(OH \bot SM\).
Ta có: \(\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot OH\)
Mà \(OH \bot SM \Rightarrow OH \bot \left( {SAB} \right) \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = OH\)
Ta có:
\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SM \bot AB\\\left( {ABCD} \right) \supset OM \bot AB\end{array} \right. \Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABCD} \right)} \right) = \angle \left( {SM;OM} \right) = \angle SMO = {60^0}\).
\(OM = \dfrac{a}{2},\,\,OH = OM.\sin \angle SMO = OM.\sin {60^0} = \dfrac{a}{2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{4}\)
\( \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = \dfrac{{a\sqrt 3 }}{4}\).
Hướng dẫn giải:
Khoảng cách từ O đến \(\left( {SAB} \right)\) là độ dài đoạn thẳng hạ vuông góc từ \(O\) đến \(\left( {SAB} \right)\).