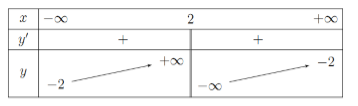
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ bên. Tìm số điểm cực trị của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\).

Ta có: \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}} \Rightarrow y' = {2019^{f\left( {f\left( x \right) - 1} \right)}}.f'\left( {f\left( x \right) - 1} \right).f'\left( x \right)\ln 2019\)

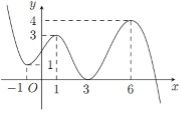
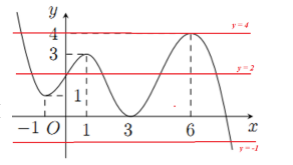
\(f'\left( {f\left( x \right) - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) - 1 =  - 1\\f\left( x \right) - 1 = 1\\f\left( x \right) - 1 = 3\\f\left( x \right) - 1 = 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}f\left( x \right) = 0\\f\left( x \right) = 2\\f\left( x \right) = 4\\f\left( x \right) = 7\end{array} \right.\)

\(f'\left( {f\left( x \right) - 1} \right) = 0\) có tất cả: \(2 + 5 + 2 + 1 = 10\) nghiệm

(trong đó, có các nghiệm \(x = 3,\,\,x = 6\) là nghiệm kép, còn lại là nghiệm đơn).

\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 1\\x = 3\\x = 6\end{array} \right.\) : có 4 nghiệm

\( \Rightarrow y' = {2019^{f\left( {f\left( x \right) - 1} \right)}}.f'\left( {f\left( x \right) - 1} \right).f'\left( x \right) = 0\) có 12 nghiệm phân biệt, trong đó, \(x = 3,\,\,x = 6\) là nghiệm bội 3, còn lại là nghiệm đơn.

Do đó, số điểm cực trị của hàm số \(y = {2019^{f\left( {f\left( x \right) - 1} \right)}}\) là 12.