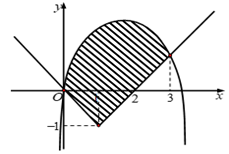
Cho $\left( H \right)$ là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình $y=\frac{10}{3}x-{{x}^{2}}$, $y=\left\{ \begin{align} & -x\,\,\,\,\,\,\,\text{khi}\,x\le 1 \\ & x-2\,\,\text{khi}\,\,x>1 \\ \end{align} \right.$. Diện tích của $\left( H \right)$ bằng?

 Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số $y={{x}^{2}}-4x+4$, trục tung và trục hoành. Xác định k để đường thẳng (d) đi qua điểm $A\left( 0;4 \right)$ và có hệ số góc k chia (H) thành hai phần có diện tích bằng nhau.

Trong không gian với hệ tọa độ $Oxyz$, cho ba điểm

$A\left( {1;2; - 1} \right),{\rm{ }}B\left( {2;1;1} \right),{\rm{ }}C\left( {0;1;2} \right)$. Gọi $H\left( {a;b;c} \right)$ là trực tâm của tam giác $ABC$. Giá trị của $a + b + c$ bằng:

Tìm phần ảo $b$ của số phức $w = \dfrac{1}{{2i}}\left( {z - \bar z} \right)$ với $z = 5 - 3i$. 

Nguyên hàm của hàm số $f\left( x \right) = \sin x + \cos x$ là :

Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} + 2x - 4y + 6z + 5 = 0$. Tiếp diện của $(S)$ tại điểm $M(-1;2;0)$ có phương trình là:

Cho hàm số $f\left( x \right)$ liên tục trên $R$ thỏa mãn $\int\limits_a^d {f\left( x \right)dx}  = 10;\int\limits_b^d {f\left( x \right)dx}  = 18;\int\limits_a^c {f\left( x \right)dx}  = 7$. Giá trị của $\int\limits_b^c {f\left( x \right)dx}$ là:

Cho số phức $z$ thỏa mãn$|z - 1 - 2i| = 4$. Gọi $M,m$ lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của $|z + 2 + i|$. Tính $S = {M^2} + {m^2}$.