Câu hỏi:
2 năm trước
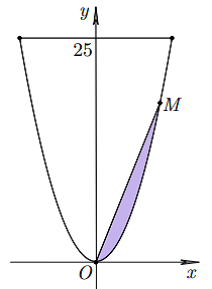
Ông B có một khu vườn giới hạn bởi đường parabol và một đường thẳng. Nếu đặt trong hệ tọa độ $Oxy$ như hình vẽ bên thì parabol có phương trình $y = {x^2}$và đường thẳng là $y = 25$. Ông B dự định dùng một mảnh vườn nhỏ được chia từ khu vườn bởi đường thẳng đi qua $O$ và điểm $M$ trên parabol để trồng hoa. Hãy giúp ông B xác định điểm $M$ bằng cách tính độ dài $OM$ để diện tích mảnh vường nhỏ bằng $\dfrac{9}{2}$.
Trả lời bởi giáo viên
Đáp án đúng: b
Giả sử $M\left( {a;{a^2}} \right) \in (P)$ thì ta có phương trình đường thẳng $OM$ là: $y = ax$
Khi đó diện tích mảnh vườn nhỏ là: $S = \int\limits_0^a {(ax - {x^2})dx = \left. {\left( {a\dfrac{{{x^2}}}{2} - \dfrac{{{x^3}}}{3}} \right)} \right|} _0^a = \dfrac{{{a^3}}}{6} = \dfrac{9}{2} \Leftrightarrow a = 3$
Khi đó ta có: $OM = 3\sqrt {10} $
Hướng dẫn giải:
- Gọi $M\left( {a;{a^2}} \right)$ và viết phương trình đường thẳng \(OM\).
- Tính diện tích hình phẳng giới hạn bởi hai đường cong \(y = f\left( x \right)\) và \(y = g\left( x \right)\):
- Bước 1: Giải phương trình \(f\left( x \right) = g\left( x \right)\) tìm nghiệm.
- Bước 2: Phá dấu giá trị tuyệt đối của biểu thức \(\left| {f\left( x \right) - g\left( x \right)} \right|\)
- Bước 3: Tính diện tích hình phẳng theo công thức tích phân \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)
