Cho hình lăng trụ $ABC.A’B’C’$ có độ dài tất cả các cạnh bằng $a$ và hình chiếu vuông góc của đỉnh $C$ trên $(ABB’A’)$ là tâm của hình bình hành $ABB’A’$. Thể tích của khối lăng trụ là:
Trả lời bởi giáo viên
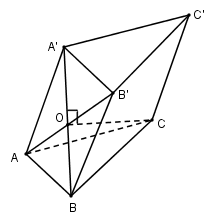
Gọi $O$ là tâm hình bình hành $ABB’A’$. Ta có \(CO \bot \left( {ABB'A'} \right) \Rightarrow CO \bot OA;CO \bot OB\)
\(\Delta COA = \Delta COB\left( {c.g.c} \right) \Rightarrow OA = OB \Rightarrow AB' = A'B \Rightarrow ABB'A'\) là hình chữ nhật.
Lại có \(AB = BB' = a \Rightarrow ABB'A'\) là hình vuông
Khi đó \(OA = OB = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }}\)
Xét tam giác vuông $OAC$ có: \(OC = \sqrt {A{C^2} - O{A^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\)
\( \Rightarrow {V_{C.A'AB}} = \dfrac{1}{3}OC.{S_{A'AB}} = \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)
Mà ${V_{ABC.A'B'C'}} = {S_{ABC}}.d\left( {A',\left( {ABC} \right)} \right) = 3.\dfrac{1}{3}{S_{ABC}}.d\left( {A',\left( {ABC} \right)} \right) = 3.{V_{A'.ABC}}$
Vậy \({V_{ABC.A'B'C'}} = 3{V_{C.A'AB}} = \dfrac{{{a^3}\sqrt 2 }}{4}\)
Hướng dẫn giải:
- Tính thể tích khối chóp \({V_{C.A'AB}}\)
- Tính thể tích khối lăng trụ dựa vào thể tích khối chóp.


