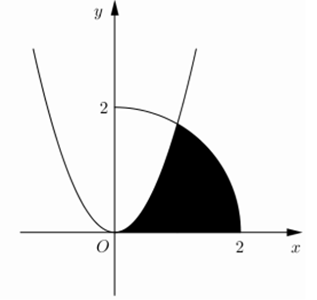
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi parabol  \(y=\sqrt{3}{{x}^{2}}\), cung tròn có phương trình \(y=\sqrt{4-{{x}^{2}}}\) (với \(0\le x\le 2\)) và trục hoành (phần tô đậm trong hình vẽ). Diện tích của \(\left( H \right)\) bằng

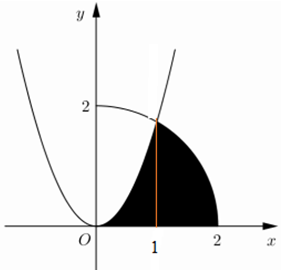
Ta có:

\(\sqrt{3}{{x}^{2}}=\sqrt{4-{{x}^{2}}}\Leftrightarrow 3{{x}^{4}}+{{x}^{2}}-4=0\Leftrightarrow \left( {{x}^{2}}-1 \right)\left( {{x}^{2}}+4 \right)=0\Leftrightarrow \left[ \begin{align}  & x=1(TM) \\  & x=-1(L) \\ \end{align} \right.\)

Do đó:

\(S=\int\limits_{0}^{1}{\sqrt{3}{{x}^{2}}dx}+\int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}dx}=\left. \frac{\sqrt{3}}{3}{{x}^{3}} \right|_{0}^{1}+\int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}dx}=\frac{\sqrt{3}}{3}+\int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}dx}\)

Tính \(I=\int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}dx}\).

Đặt \(x=2\sin t\Rightarrow dx=2\cos tdt\).

Đổi cận \(\left\{ \begin{align}  & x=1\Rightarrow \sin t=\frac{1}{2}\Rightarrow t=\frac{\pi }{6} \\  & x=2\Rightarrow \sin t=1\Rightarrow t=\frac{\pi }{2} \\ \end{align} \right.\)

\(\begin{align}  & I=\int\limits_{1}^{2}{\sqrt{4-{{x}^{2}}}dx}=\int\limits_{\pi /6}^{\pi /2}{\sqrt{4-4{{\sin }^{2}}t}.2\cos tdt}=\int\limits_{\pi /6}^{\pi /2}{4{{\cos }^{2}}tdt}=\int\limits_{\pi /6}^{\pi /2}{2\left( \cos 2t+1 \right)dt} \\  & =\left. \sin 2t \right|_{\pi /6}^{\pi /2}+\left. 2t \right|_{\pi /6}^{\pi /2}=\frac{2\pi }{3}-\frac{\sqrt{3}}{2} \\ \end{align}\)

Suy ra \(S=\frac{\sqrt{3}}{3}+\frac{2\pi }{3}-\frac{\sqrt{3}}{2}=\frac{4\pi -\sqrt{3}}{6}\).