Cho hai mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {y^2} + {\left( {z - 3} \right)^2} = 36\) và \(\left( {S'} \right):{\left( {x + 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 81\). Gọi \(d\) là đường thẳng tiếp xúc với cả hai mặt cầu trên và cách điểm \(M\left( {4; - 1; - 7} \right)\) một khoảng lớn nhất. Gọi \(E\left( {m;n;p} \right)\) là giao điểm của \(d\) với mặt phẳng \(\left( P \right):2x - y + z - 17 = 0\). Biểu thức \(T = m + n + p\) có giá trị bằng

Mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;0;3} \right)\) và có bán kính \(R = 6\).

Mặt cầu \(\left( {S'} \right)\) có tâm \(K\left( { - 1;1;1} \right)\) và có bán kính \(R' = 9\).

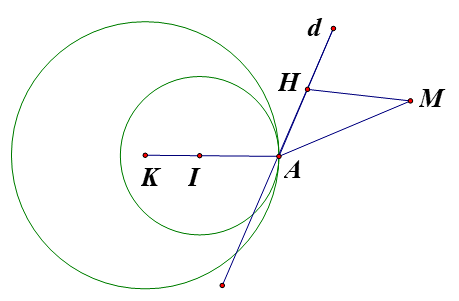
Lại có \(\overrightarrow {KI}  = \left( {2; - 1;2} \right) \Rightarrow KI = \sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {2^2}}  = 3 \Rightarrow KI = R' - R\) suy ra hai mặt cầu tiếp xúc trong tại điểm \(A\left( {a;b;c} \right)\), mà \(KA = R' = 9 = 3KI \Rightarrow \overrightarrow {KA}  = 3\overrightarrow {KI} \) \( \Rightarrow \left\{ \begin{array}{l}a + 1 = 6\\b - 1 =  - 3\\c - 1 = 6\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 5\\b =  - 2\\c = 7\end{array} \right.\).

Do đó \(A\left( {5; - 2;7} \right)\). Vì \(d\) là đường thẳng tiếp xúc với cả hai mặt cầu trên nên \(d\) đi qua \(A\) và vuông góc với \(KI\). Kẻ \(MH \bot d \Rightarrow MH \le MA\), nên \(MH\) lớn nhất khi và chỉ khi \(H\) trùng \(A\).

Khi đó \(d\) là đường thẳng đi qua \(A\) và vuông góc với \(KI\) và \(AM\) suy ra \(d\) có một véc tơ chỉ phương \(\overrightarrow u  = \left[ {\overrightarrow {KI} ,\overrightarrow {AM} } \right]\). Ta có \(\overrightarrow {AM}  = \left( { - 1;1; - 14} \right) \Rightarrow \overrightarrow u  = \left( {12;26;1} \right)\).

Nên phương trình tham số của \(d\) là \(\left\{ \begin{array}{l}x = 5 + 12t\\y =  - 2 + 26t\\z = 7 + t\end{array} \right.\).

Vì \(E = d \cap \left( P \right)\) suy ra \(E\left( {5 + 12t; - 2 + 26t;7 + t} \right)\), Vì \(E \in \left( P \right)\) suy ra \(2\left( {5 + 12t} \right) - \left( { - 2 + 26t} \right) + \left( {7 + t} \right) - 17 = 0\) \( \Leftrightarrow t = 2\). Suy ra \(E\left( {29;50;9} \right)\).

Mà \(E\left( {m;n;p} \right)\)suy ra \(\left\{ \begin{array}{l}m = 29\\n = 50\\p = 9\end{array} \right.\). Vậy \(T = 88\).