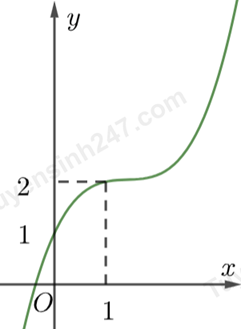
Cho hàm số bậc ba \(y = f\left( x \right)\) có đồ thị là đường cong trong hình bên dưới:

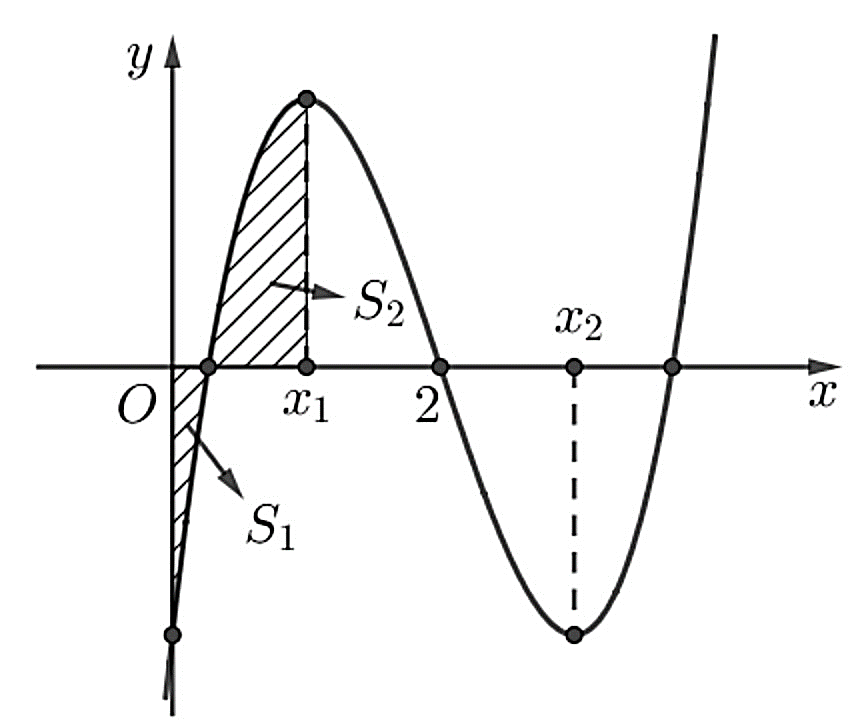
Biết hàm số \(f\left( x \right)\) đạt cực trị tại các điểm \({x_1},\,\,{x_2}\) sao cho \({x_2} - {x_1} = 2\) và \(f''\left( 2 \right) = 0\). Gọi \({S_1}\) và \({S_2}\) là diện tích hai hình phẳng được gạch trong hình bên. Tỉ số \(\dfrac{{{S_1}}}{{{S_2}}}\) bằng

Đặt \(f\left( x \right) = a{x^3} + b{x^2} + cx + d,\,\,\left( {a > 0} \right)\) \( \Rightarrow f'\left( x \right) = 3a{x^2} + 2bx + c\) \( \Rightarrow f''\left( x \right) = 6ax + 2b\).

\(f''\left( x \right) = 0 \Leftrightarrow 6ax + 2b = 0 \Leftrightarrow x = \dfrac{{ - b}}{{3a}}\). Vì \(f''\left( 2 \right) = 0\) nên \(\dfrac{{ - b}}{{3a}} = 2 \Leftrightarrow b =  - 6a\).

Mặt khác, theo định lý Vi-et thì \({x_1} + {x_2} = \dfrac{{ - 2b}}{{3a}} = 4\), kết hợp với \({x_2} - {x_1} = 2\) ta suy ra \({x_1} = 1,\,\,{x_2} = 3\)

Do đó, \({x_1}.{x_2} = \dfrac{c}{{3a}} = 3 \Leftrightarrow c = 9a\). Từ đó ta có \(f\left( x \right) = a{x^3} - 6a{x^2} + 9ax + d\).

Từ đồ thị hàm số ta suy ra \(f\left( 2 \right) = 0\) \( \Leftrightarrow 8a - 24a + 18a + d = 0 \Leftrightarrow d =  - 2a\).

Suy ra \(f\left( x \right) = a\left( {{x^3} - 6{x^2} + 9x - 2} \right)\).

Xét phương trình \(f\left( x \right) = 0 \Leftrightarrow {x^3} - 6{x^2} + 9x - 2 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 2 - \sqrt 3  < 2\\x = 2 + \sqrt 3  > 2\end{array} \right.\)

Từ đây ta tính được \({S_1} =  - a\int\limits_0^{2 - \sqrt 3 } {\left( {{x^3} - 6{x^2} + 9x - 2} \right)dx}  = \dfrac{a}{4},\) \({S_2} = a\int\limits_{2 - \sqrt 3 }^1 {\left( {{x^3} - 6{x^2} + 9x - 2} \right)dx}  = a\)

Vậy \(\dfrac{{{S_1}}}{{{S_2}}} = \dfrac{1}{4}\).