Xét hai số phức \({z_1}\,,\,{z_2}\) thỏa mãn \(2\left| {{{\bar z}_1} + i} \right| = \left| {{{\bar z}_1} - {z_1} - 2i} \right|\) và \(\left| {{z_2} - i - 10} \right| = 1\). Giá trị nhỏ nhất của biểu thức \(\left| {{z_1} - {z_2}} \right|\) bằng

Gọi \({z_1} = x + yi{\rm{ }}\left( {x,y \in \mathbb{R}} \right)\). Ta có \(2\left| {{{\bar z}_1} + i} \right| = \left| {{{\bar z}_1} - {z_1} - 2i} \right|\) \( \Leftrightarrow 2\left| {x + (1 - y)i} \right| = \left| { - 2(y + 1)i} \right|\) \( \Leftrightarrow {x^2} + {(1 - y)^2} = {(y + 1)^2} \Leftrightarrow y = \dfrac{{{x^2}}}{4}\).

\( \Rightarrow \)Tập hợp điểm \(M\) biểu diễn \({z_1}\) là parabol \(\left( P \right)\,:\,y = \dfrac{1}{4}{x^2}\) có đỉnh \(O\left( {0\,;\,0} \right)\).

\(\left| {{z_2} - i - 10} \right| = 1 \Rightarrow \)Tập hợp điểm \(N\) biễu diễn \({z_2}\) là đường tròn \(\left( C \right)\) có tâm \(I\left( {10\,;\,1} \right)\,\)bán kính \(R = 1\).

Khi đó \(P = \left| {{z_1} - {z_2}} \right| = MN\) là khoảng cách từ một điểm thuộc \(\left( P \right)\) đến một điểm thuộc \(\left( C \right)\).

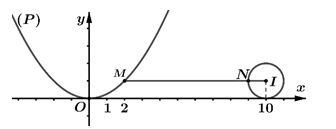
Ta có: \(MN + NI \ge MI\) \( \Rightarrow MN \ge MI - NI = MI - 1\)\( \Rightarrow M{N_{\min }} \Leftrightarrow I{M_{\min }}\).

Mà \(I{M^2} = {\left( {x - 10} \right)^2} + {\left( {\dfrac{{{x^2}}}{4} - 1} \right)^2}\).

\( = {\left( {\dfrac{{{x^2}}}{4} - 4} \right)^2} + \dfrac{5}{2}{\left( {x - 4} \right)^2} + 45 \ge 45\) \( \Rightarrow IM \ge \sqrt {45}  = 3\sqrt 5 \).

Do đó \(M{N_{\min }} = 3\sqrt 5  - 1\).