Cho hàm số \(y = f(x)\) có đạo hàm \(f'(x) = {\left( {x - 1} \right)^2}\left( {{x^2} - 2x} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g(x) = f\left( {{x^2} - 8x + m} \right)\) có đúng \(5\) điểm cực trị?

Xét \(f'(x) = 0 \Leftrightarrow {(x - 1)^2}\left( {{x^2} - 2x} \right) = 0\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1\,\,({\text{ nghiệm bội }}2)}\\{x = 0}\\{x = 2}\end{array}} \right.\)

Ta có: \(g'(x) = 2(x - 4).f'\left( {{x^2} - 8x + m} \right)\)

\(g'(x) = 0 \Leftrightarrow 2(x - 4) \cdot f'\left( {{x^2} - 8x + m} \right) = 0\) \( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 4}\\{{x^2} - 8x + m = 1\,\,({\text{ nghiệm bội }}2)}\\{{x^2} - 8x + m = 0\,\,(1)}\\{{x^2} - 8x + m = 2\,\,(2)}\end{array}} \right.\)

Yêu cầu bài toán trở thành \(g'(x) = 0\) có \({\rm{5}}\) nghiệm bội lẻ hay mỗi phương trình (1), (2) đều có hai nghiệm phân biệt khác 4. (*)

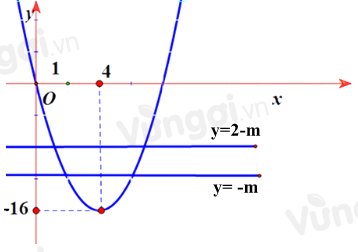
Xét đồ thị \(({\rm{C}})\) của hàm số \(y = {x^2} - 8x\) và hai đường thẳng \({d_1}:y =  - m\); \({d_2}:y =  - m + 2\) (như hình vẽ).

Khi đó (*) xảy ra khi \({d_1},\;{d_2}\) cắt \(({\rm{C}})\) tại 4 điểm phân biệt \( \Leftrightarrow  - m >  - 16\) \( \Leftrightarrow m < 16\)

Vậy có \({\rm{15}}\) giá trị \(m\) nguyên dương thỏa mãn: \(\{ 1,2,3,..,15\} .\)