Câu hỏi:
2 năm trước
Cho lăng trụ đều \(ABC.A'B'C'\), cạnh đáy bằng a, góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính thể tích khối lăng trụ đó.
Trả lời bởi giáo viên
Đáp án đúng: c
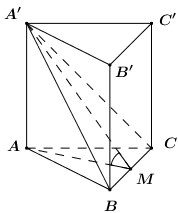
Gọi \(M\) là trung điểm của \(BC\). Ta có:
\(AM \bot BC\) (do \(\Delta ABC\) đều)
\(BC \bot AA'\,\,\left( {gt} \right)\)
\( \Rightarrow BC \bot \left( {AA'M} \right) \Rightarrow BC \bot A'M\).
Ta có: \(\left\{ \begin{array}{l}\left( {A'BC} \right) \cap \left( {ABC} \right) = BC\\AM \subset \left( {ABC} \right),\,\,AM \bot BC\\A'M \subset \left( {A'BC} \right),\,\,A'M \bot BC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {A'BC} \right);\left( {ABC} \right)} \right) = \angle \left( {A'M;AM} \right) = \angle A'MA = {60^0}\).
Vì \(\Delta ABC\) đều cạnh \(a\) nên \(AM = \dfrac{{a\sqrt 3 }}{2}\) và \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Xét tam giác vuông \(A'AM\) có: \(AA' = AM.\tan {60^0} = \dfrac{{a\sqrt 3 }}{2}.\sqrt 3 = \dfrac{{3a}}{2}\).
Vậy thể tích khối lăng trụ là \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = \dfrac{{3a}}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^2}\sqrt 3 }}{8}\).
Hướng dẫn giải:
- Gọi \(M\) là trung điểm của \(BC\), chứng minh \(\angle \left( {\left( {A'BC} \right);\left( {ABC} \right)} \right) = \angle A'MA\).
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính chiều cao \(AA'\).
- Tính thể tích khối lăng trụ \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}}\).
Câu hỏi khác
- Đề thi kiểm tra giữa học kì 1 - Đề số 5 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 3 Toán 12 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 đề số 2 Toán 12 có lời giải chi tiết
