Câu hỏi:
2 năm trước
Hàm số $y = {x^3} - 6{x^2} + mx + 1$ đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right)$ khi giá trị của $m$ là:
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có $y' = 3{x^2} - 12x + m$. Để hàm số đồng biến trên $\left( {0; + \infty {\rm{\;}}} \right)$ thì $y' \ge 0{\mkern 1mu} ,\forall x > 0$
$ \Leftrightarrow 3{x^2} - 12x + m \ge 0,{\mkern 1mu} \forall x > 0 \Leftrightarrow - 3{x^2} + 12x \le m,\forall x > 0$. (*)
Xét $y = g\left( x \right) = - 3{x^2} + 12x$ với $x > 0$.
Ta có $g'\left( x \right) = - 6x + 12 = 0 \Leftrightarrow x = 2$(TM).
BBT $y = g\left( x \right)$ với $x > 0$.
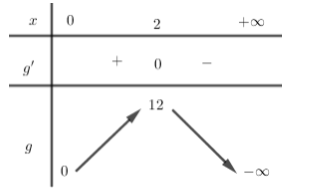
Từ BBT ta có $\mathop {\max }\limits_{\left( {0; + \infty {\rm{\;}}} \right)} {\mkern 1mu} g\left( x \right) = 12$, từ (*) suy ra $m \ge \mathop {\max }\limits_{\left( {0; + \infty {\rm{\;}}} \right)} {\mkern 1mu} g\left( x \right) = 12 \Leftrightarrow m \ge 12$.
Hướng dẫn giải:
Hàm số $y = a{x^3} + b{x^2} + cx + d,{\mkern 1mu} \left( {a \ne 0} \right)$ đồng biến trên $\left( {p;q} \right)$ khi và chỉ khi $y' \ge 0,{\mkern 1mu} \forall x \in \left( {p;q} \right)$.
Câu hỏi khác
- Đề thi kiểm tra giữa học kì 1 - Đề số 5 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 1 Toán 12 có lời giải chi tiết
- Đề thi kiểm tra giữa học kì 1 - Đề số 3 Toán 12 có lời giải chi tiết
- Đề kiểm tra giữa học kì 2 đề số 2 Toán 12 có lời giải chi tiết
