Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ như hình vẽ bên
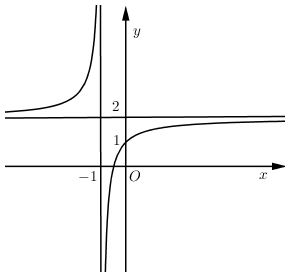
Chọn khẳng định đúng:
Trả lời bởi giáo viên
Đồ thị hàm số $y = \dfrac{{2x + b}}{{cx + d}}$ có $\left\{ \begin{align}& \xrightarrow{TCN}y=\dfrac{2}{c}=2\Rightarrow c=1 \\ & \xrightarrow{TCD}x=-\dfrac{d}{c}=-\dfrac{d}{1}=-1\Rightarrow d=1 \\ \end{align} \right.$
Hàm số có dạng $y = \dfrac{{2x + b}}{{x + 1}}\left( C \right)$
Ta có điểm $\left( {0;1} \right) \in \left( C \right)$
Thay $x = 0$ và $y = 1$ vào hàm số ta được $1 = \dfrac{{2.0 + b}}{{0 + 1}} \Rightarrow b = 1$ $ \Rightarrow b + c + d = 3$
Hướng dẫn giải:
- Tìm các tiệm cận đứng, ngang của đồ thị hàm số $ \Rightarrow c,d$.
- Tìm điểm đi qua của đồ thị hàm số $ \Rightarrow b$.
- Thay các giá trị tìm được vào kiểm tra các đáp án.
Giải thích thêm:
HS thường nhầm lẫn trong việc xác định tiệm cận đứng $x = \dfrac{d}{c}$ dẫn đến tính ra $d = - 1$ và chọn nhầm đáp án A là sai.


