Cho hàm số \(f\left( x \right)={{x}^{3}}-3{{x}^{2}}.\) Có bao nhiêu giá trị nguyên của \(m\) để đồ thị hàm số \(g\left( x \right)=f\left( \left| x \right| \right)+m\) cắt trục hoành tại 4 điểm phân biệt ?
Trả lời bởi giáo viên
Dựa vào đồ thị hàm số \(f\left( \left| x \right| \right)={{\left| x \right|}^{3}}-3{{\left| x \right|}^{2}},\) hình vẽ bên dưới:
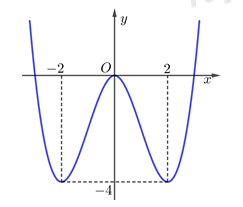
Để phương trình \(g\left( x \right)=0\Leftrightarrow f\left| \left( x \right) \right|=-\,m\) có 4 nghiệm phân biệt \(\Leftrightarrow \)\(-\,4<-\,m<0\Leftrightarrow 0<m<4.\)
Kết hợp với điều kiện \(m\in \mathbb{Z}\)\(\xrightarrow{{}}\,\,m=\left\{ 1;\,\,2;\,\,3 \right\}\) là các giá trị cần tìm.
Hướng dẫn giải:
Dựa vào đồ thị hàm số \(y=f\left( \left| x \right| \right)\) được vẽ thông qua đồ thị hàm số\(y=f\left( x \right)\) xác định giá trị tham số để phương trình đã cho có 4 nghiệm phân biệt

