Cho lăng trụ $ABC.A'B'C'$ có đáy $ABC$ là tam giác đều cạnh $a$, và \(A'A = A'B = A'C = a\sqrt {\dfrac{7}{{12}}} \) . Thể tích khối lăng trụ \(ABC.A'B'C'\) theo $a$ là:
Trả lời bởi giáo viên
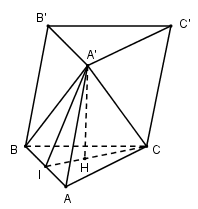
Gọi $H$ là tâm tam giác đều $ABC$ . Vì $A'A = A'B = A'C$ nên hình chóp $A'.ABC$ là đều nên \(A'H \bot \left( {ABC} \right)\)
Gọi $I$ là trung điểm của $AB$.
Vì tam giác $ABC$ đều cạnh $a$ nên \(CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow HI = \dfrac{1}{3}CI = \dfrac{{a\sqrt 3 }}{6}\)
Tam giác $A'AB$ cân tại $A'$ nên \(A'I \bot AB \Rightarrow \Delta A'AI\) vuông tại \(I \Rightarrow A'I = \sqrt {AA{'^2} - A{I^2}} = \sqrt {\dfrac{{7{a^2}}}{{12}} - \dfrac{{{a^2}}}{4}} = \dfrac{a}{{\sqrt 3 }}\)
\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot HI \Rightarrow \Delta A'HI\) vuông tại \(H \Rightarrow A'H = \sqrt {A'{I^2} - H{I^2}} = \sqrt {\dfrac{{{a^2}}}{3} - \dfrac{{{a^2}}}{{12}}} = \dfrac{a}{2}\)
Vì tam giác $ABC$ đều cạnh $a$ nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\)
Hướng dẫn giải:
- Tính diện tích đáy \({S_{ABC}}\).
- Xác định chiều cao của khối lăng trụ dựa vào tính chất của hình chóp đều.
- Tính thể tích khối lăng trụ theo công thức \(V = Sh\) với \(S\) là diện tích đáy và \(h\) là chiều cao.

