Câu hỏi:
2 năm trước
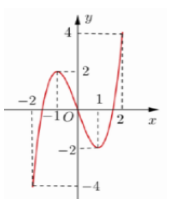
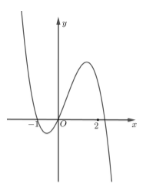
Cho hàm số f(x)=ax4+bx3+cx2+dx+e, với a,b,c,d,e∈R. Hàm số y=f′(x) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có f′(x)=4ax3+3bx2+2cx+d
Từ đồ thị hàm số ta thấy f′(0)⇔d=0
Từ đồ thị ta thấy:
+ Khi x<−1 thì f′(x)>0.
+ Khi −1<x<0=>f′(x)<0
+ Khi 0<x<x0 (với x0 là nghiệm thứ 3 của phương trình f′(x)=0) =>f′(x)>0
+ Khi x>x0 thì f′(x)<0
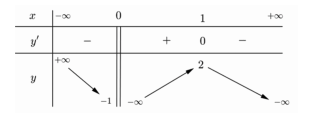
Ta có bảng biến thiên:
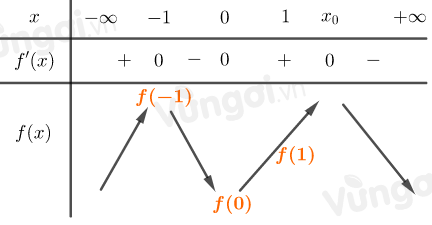
⇒f(−1)>f(0)
⇔a−b+c−d+e>e⇔a+c>b+d nên B sai, lại có d=0⇒a+c>b (1)
+) Từ bảng biến thiên ⇒f(1)>f(0)
⇔a+b+c+d+e>e⇔a+b+c+d>0 nên A sai.
Mà d=0 nên a+b+c>0⇔a+c>−b (2)
Từ (1) và (2) suy ra 2(a+c)>0⇔a+c>0.
Hướng dẫn giải:
Từ đồ thị hàm số suy ra f′(0)=0;f′(x)>0,∀x∈(0;1)
Lập bảng biến thiên của hàm số y=f(x)