Cho bất phương trình \(\sqrt[3]{{{x^4} + {x^2} + m}} - \sqrt[3]{{2{x^2} + 1}} + {x^2}\left( {{x^2} - 1} \right) > 1 - m\). Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình nghiệm đúng với mọi \(x > 1.\)
Trả lời bởi giáo viên
Ta có \(\sqrt[3]{{{x^4} + {x^2} + m}} - \sqrt[3]{{2{x^2} + 1}} + {x^2}\left( {{x^2} - 1} \right) > 1 - m\)
\( \Leftrightarrow \sqrt[3]{{{x^4} + {x^2} + m}} - \sqrt[3]{{2{x^2} + 1}} + {x^4} - {x^2} > 1 - m\)
\( \Leftrightarrow \sqrt[3]{{{x^4} + {x^2} + m}} + {x^4} + {x^2} + m > \sqrt[3]{{2{x^2} + 1}} + 2{x^2} + 1\) (*)
Xét hàm số \(f\left( t \right) = {t^3} + t\,\,\, \Rightarrow y' = 2{t^2} + 1 > 0\) nên hàm số \(f\left( t \right)\) là hàm đồng biến
Khi đó phương trình (*) trở thành:
\(f\left( {\sqrt[3]{{{x^4} + {x^2} + m}}} \right) > f\left( {\sqrt[3]{{2{x^2} + 1}}} \right)\) \( \Leftrightarrow \sqrt[3]{{{x^4} + {x^2} + m}} > \sqrt[3]{{2{x^2} + 1}}\) \( \Leftrightarrow {x^4} + {x^2} + m > 2{x^2} + 1\) \( \Leftrightarrow m > {\rm{\;}} - {x^4} + {x^2} + 1\)
Xét hàm số \(g\left( x \right) = - {x^4} + {x^2} + 1\) với \(x > 1\)
Có \(g'\left( x \right) = - 4{x^3} + 2x = - 2x\left( {2{x^2} - 1} \right) < 0;\,\forall x > 1\)
Ta có BBT của hàm \(g\left( x \right) = - {x^4} + {x^2} + 1\) với \(x > 1\)
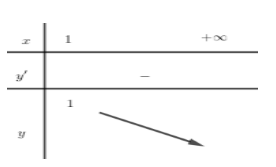
Từ BBT suy ra \(m \ge 1.\)
Hướng dẫn giải:
- Biến đổi phương trình đã cho về dạng \(f\left( u \right) > f\left( v \right) \Leftrightarrow u > v\) với \(f\left( t \right)\) là hàm đơn điệu tăng.
- Từ đó cô lập m đưa về dạng \(g\left( x \right) > m\) với mọi \(x > 1\)
- Lập BBT của hàm số \(y = g\left( x \right)\) trên \(\left( {1; + \infty } \right)\) rồi kết luận.
Giải thích thêm:
Các em có thể biến đổi theo cách nhân chia với biểu thức liên hợp dưới đây:
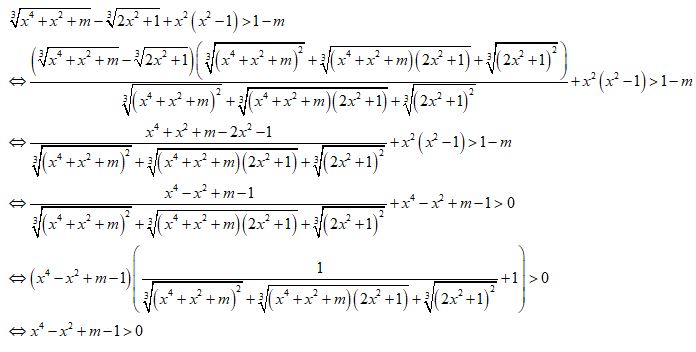
Đến đây các em làm tiếp theo lời giải phía trên sẽ được kết quả nhé!