Cho hình chóp tam giác đều $S.ABC$ có $SA = 2a,AB = 3a.$ Gọi $M$ là trung điểm $SC.$ Tính khoảng cách từ $M$  đến mặt phẳng  $\left( {SAB} \right)$.

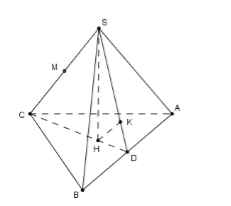
Gọi $D$ là trung điểm của $AB,\,\,H$ là trọng tâm tam giác $ABC$.

Khi đó $SH \bot \left( {ABC} \right)$ do $S.ABC$ là hình chóp đều.

Kẻ $HK \bot SD$ tại $K.$

Ta có $\left\{ \begin{array}{l}AB \bot CD\,\,\left( {do\,\,\Delta ABC\,\,deu} \right)\\AB \bot SH\left( {do\,SH \bot \left( {ABC} \right)} \right)\end{array} \right. \Leftrightarrow AB \bot \left( {SDC} \right) \Rightarrow AB \bot HK$

Mà $HK \bot SD \Rightarrow HK \bot \left( {SAB} \right)$ tại $K \Rightarrow d\left( {H,\left( {SAB} \right)} \right) = HK$

+) Vì tam giác $ABC$ đều cạnh $3a$ nên

$CD = \dfrac{{\sqrt 3 }}{2}.3a = \dfrac{{3\sqrt 3 a}}{2} \Rightarrow HD = \dfrac{1}{3}CD = \dfrac{{\sqrt 3 }}{2}a;\,\,HC = \dfrac{2}{3}CD = \sqrt 3 a$

Vì $S.ABC$ là chóp đều nên $SC = SA = 2a$ .

Xét tam giác $SHC$ vuông tại $C,$ theo định lý Pytago ta có $SH = \sqrt {S{C^2} - H{C^2}}  = \sqrt {4{a^2} - 3{a^2}}  = a$.

+) Xét tam giác $SHD$ vuông tại $H,$ ta có $\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{D^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{\dfrac{3}{4}{a^2}}} = \dfrac{7}{{3{a^2}}} \Rightarrow HK = \dfrac{{a\sqrt {21} }}{7}$

+) Ta có $\dfrac{{d\left( {C,\left( {SAB} \right)} \right)}}{{d\left( {H,\left( {SAB} \right)} \right)}} = \dfrac{{CD}}{{HD}} = 3 \Leftrightarrow d\left( {C;\left( {SAB} \right)} \right) = 3.d\left( {H;\left( {SAB} \right)} \right) = \dfrac{{3a\sqrt {21} }}{7}$.

Lại có $\dfrac{{d\left( {M,\left( {SAB} \right)} \right)}}{{d\left( {C,\left( {SAB} \right)} \right)}} = \dfrac{{MA}}{{CA}} = \dfrac{1}{2} \Leftrightarrow d\left( {M;\left( {SAB} \right)} \right) = \dfrac{1}{2}.d\left( {C;\left( {SAB} \right)} \right) = \dfrac{{3a\sqrt {21} }}{{14}}$