Câu hỏi:
2 năm trước
Cho hàm số \(f\left( x \right) = {x^2}\left( {x - 1} \right){e^{3x}}\) có một nguyên hàm là hàm số \(F\left( x \right).\) Số cực trị của hàm số \(F\left( x \right)\) là
Trả lời bởi giáo viên
Đáp án đúng: a
Vì hàm số \(f\left( x \right) = {x^2}\left( {x - 1} \right){e^{3x}}\) có một nguyên hàm là hàm số \(F\left( x \right)\) nên \(F'\left( x \right) = f\left( x \right) = {x^2}\left( {x - 1} \right){e^{3x}}\)
Xét \(F'\left( x \right) = 0 \Leftrightarrow {x^2}\left( {x - 1} \right){e^{3x}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\end{array} \right.\)
Bảng biến thiên của hàm \(F\left( x \right).\)
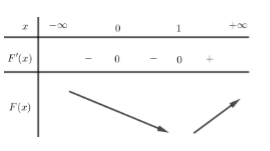
Vậy hàm số có 1 điểm cực trị.
Hướng dẫn giải:
Sử dụng \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) \Rightarrow F'\left( x \right) = f\left( x \right)\)
Từ đó ta lập bảng xét dấu của hàm \(F'\left( x \right)\) để tìm số cực trị của hàm số \(F\left( x \right)\)
Câu hỏi khác
- Đề thi thử THPTQG môn Toán Chuyên ĐH Vinh Nghệ An lần 3 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 2 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 1 Toán 12 có lời giải chi tiết
- Đề tập huấn thi THPTQG Sở Giáo Dục và Đào Tạo Bắc Ninh 2019 Toán 12 có lời giải chi tiết
- Đề thi thử THPTQG - Đề số 4 Toán 12 có lời giải chi tiết
