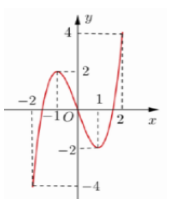
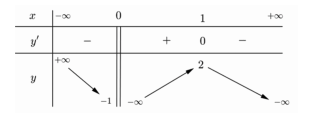
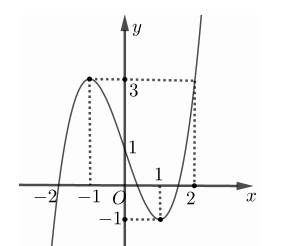
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ dưới đây. Gọi \(S\) là tập hợp tất cả các giá trị của tham số \(m\) để phương trình \(f\left( {3 - \sqrt {4 - {x^2}} } \right) = m\) có hai nghiệm phân biệt thuộc đoạn \(\left[ { - \sqrt 2 ;\sqrt 3 } \right]\). Tìm tập \(S\).

Đặt \(t = 3 - \sqrt {4 - {x^2}} \) \( \Rightarrow 3 - t = \sqrt {4 - {x^2}}  \Leftrightarrow \left\{ \begin{array}{l}t \le 3\\{x^2} = 4 - {\left( {3 - t} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t \le 3\\{x^2} = \left( {t - 1} \right)\left( {5 - t} \right) \ge 0\end{array} \right. \Rightarrow 1 \le t \le 3\)

Nhận thấy với \(t = 1\) thì \({x^2} = 0 \Leftrightarrow x = 0\) hay với \(t = 1\) thì ta chỉ tìm được đúng một nghiệm \(x\) (loại)

Với \(1 < t \le 3\) thì \({x^2} > 0\) nên ta sẽ tìm được hai giá trị của \(x\) đối nhau.

Do đó để phương trình có hai nghiệm phân biệt thuộc đoạn \(\left[ { - \sqrt 2 ;\sqrt 3 } \right]\) thì phương trình phải có hai nghiệm phân biệt đối nhau thuộc \(\left[ { - \sqrt 2 ;\sqrt 2 } \right]\) và \(x \ne 0\).

Dễ thấy \(x \in \left[ { - \sqrt 2 ;\sqrt 2 } \right]\backslash \left\{ 0 \right\} \Rightarrow {x^2} \in \left( {0;2} \right] \Rightarrow 4 - {x^2} \in \left[ {2;4} \right)\)

\( \Rightarrow \sqrt {4 - {x^2}}  \in \left[ {\sqrt 2 ;2} \right) \Rightarrow 3 - \sqrt {4 - {x^2}}  \in \left( {1;3 - \sqrt 2 } \right]\)

\( \Rightarrow t \in \left( {1;3 - \sqrt 2 } \right] \Rightarrow f\left( t \right) \in \left( {f\left( 1 \right);f\left( {3 - \sqrt 2 } \right)} \right]\) vì \(f\left( t \right)\) đồng biến trên \(\left( {1;3 - \sqrt 2 } \right]\).

Phương trình đã cho có hai nghiệm \({x_1},{x_2}\) phân biệt thuộc đoạn \(\left[ { - \sqrt 2 ;\sqrt 3 } \right]\) thì phương trình \(f\left( t \right) = m\) có nghiệm duy nhất \(t \in \left( {1;3 - \sqrt 2 } \right]\)

\( \Rightarrow m = f\left( t \right) \in \left( {f\left( 1 \right);f\left( {3 - \sqrt 2 } \right)} \right] = \left( { - 1;f\left( {3 - \sqrt 2 } \right)} \right]\).

Vậy \(S = \left( { - 1;f\left( {3 - \sqrt 2 } \right)} \right]\).