Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 18cm, dao động theo phương thẳng đứng với phương trình là uA=uB=A.cos50πt (với t tính bằng s). Tốc độ truyền sóng ở mặt chất lỏng là 50cm/s. Gọi O là trung điểm của AB, điểm M ở mặt chất lỏng nằm trên đường trung trực của AB và gần O nhất sao cho phần tử chất lỏng tại M dao động cùng pha với phần tử chất lỏng tại O. Khoảng cách MO là
Ta có: {f=25Hzv=50cm/s⇒λ=vf=2cm
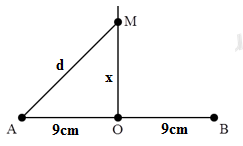
Phương trình dao động tại O:
uO=2A.cos(50πt−2π.OAλ)=2A.cos(50πt−2π.92)=2A.cos(50πt−9π)
Phương trình dao động tại M:
uM=2A.cos(50πt−2π.OMλ)=2A.cos(50πt−2π.d2)=2A.cos(50πt−πd)
M dao động cùng pha với O nên:
Δφ=πd−9π=k2π⇒d=9+2kd>9cm⇔9+2k>9⇒k>0⇒k=1;2;3;...dmin⇔k=1⇒d=9+2=11cm
Áp dụng định lí Pitago ta có: xmin=√d2min−92=√112−92=√40=2√10cm
Hai nguồn sóng kết hợp trên mặt nước S1, S2 dao động với phương trình:
u1=asin(ωt),u2=acos(ωt);S1S2=9λ . Điểm M gần nhất trên trung trực của S1S2 dao động cùng pha với u1 cách S1, S2 bao nhiêu.
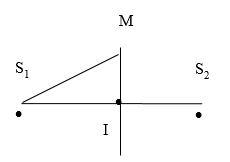
Ta có:
u1=asinωt=acos(ωt−π2);u2=acos(ωt)
Xét điểm M trên trung trực của S1S2:
S1M=S2M=d(d⩾
\begin{array}{l}{u_{1M}} = acos(\omega t - \frac{\pi }{2} - \frac{{2\pi d}}{\lambda });{u_{2M}} = acos(\omega t - \frac{{2\pi d}}{\lambda })\\{u_M} = {u_{1M}} + {\rm{ }}{u_{2M}} = acos(\omega t - \frac{{2\pi d}}{\lambda } - \frac{\pi }{2}) + {\rm{ }}acos(\omega t - \frac{{2\pi d}}{\lambda })\\{u_M} = 2{\rm{acos(}}\frac{\pi }{4})c{\rm{os}}\left( {\omega t - \frac{{2\pi d}}{\lambda } - \frac{\pi }{4}} \right)\end{array}
Để M dao động cùng pha với u1:
\begin{array}{l}\frac{{2\pi d}}{\lambda } + \frac{\pi }{4} - \frac{\pi }{2} = 2k\pi \to d = \left( {\frac{1}{8} + k} \right)\lambda \\ \to d = (\frac{1}{8} + k)\lambda \ge 4,5\lambda \to k \ge 4,375 \to k \ge 5\end{array}
\begin{array}{*{20}{l}}{ = > {\text{ }}{k_{min}} = {\text{ }}5} \\{ = > {\text{ }}{d_{min}} = {\text{}}41\lambda /8}\end{array}
Hai nguồn phát sóng kết hợp S1, S2 trên mặt nước cách nhau 30 cm phát ra hai dao động điều hoà cùng phương, cùng tần số f = 50 Hz và pha ban đầu bằng không. Biết tốc độ truyền sóng trên mặt chất lỏng v = 6m/s. Những điểm nằm trên đường trung trực của đoạn S1S2 mà sóng tổng hợp tại đó luôn dao động ngược pha với sóng tổng hợp tại O ( O là trung điểm của S1S2) cách O một khoảng nhỏ nhất là:
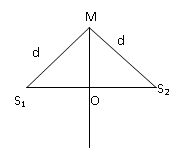
Giả sử hai sóng tại S1, S2 có dạng :
{u_1} = {\rm{ }}{u_2} = {\rm{ }}acos\omega t
Gọi M là 1 điểm thỏa mãn bài toán (có 2 điểm thỏa mãn nằm đối xứng nhau qua S1,S2)
Phương trình dao động tại M:
{u_M} = 2acos(\omega t - \frac{{2\pi d}}{\lambda }) (d: Khoảng cách từ M đến S1, S2)
Phương trình dao động tại O:
{u_O} = 2acos(\omega t - \frac{{2\pi {\rm{O}}{{\rm{S}}_1}}}{\lambda })
Theo bài ra:
\begin{array}{l}\Delta {\varphi _{M/O}} = {\varphi _M} - {\varphi _O} = \frac{{2\pi }}{\lambda }({\rm{O}}{{\rm{S}}_1} - d) = (2k + 1)\pi \to {\rm{O}}{{\rm{S}}_1} - d = \frac{\lambda }{2}(2k + 1)\\ \to d = {\rm{O}}{{\rm{S}}_1} - \frac{\lambda }{2}(2k + 1){\rm{ (*)}}\end{array}
Tam giác S1OM vuông nên:
\begin{gathered}d{\text{ }} > {\text{ }}O{S_1} \to {\text{O}}{{\text{S}}_1} - \frac{\lambda }{2}(2k + 1) > {\text{ }}O{S_1} \hfill \\\leftrightarrow 2k + 1 < 0 \to k < - \frac{1}{2}(k \in Z) \hfill \\\end{gathered}
Nhìn vào biểu thức (*) ta thấy dmin khi kmax = -1. (do OS1 không đổi nên dmin thì OM min )
Thay OS1 = S1S2/2 = 15cm;
\lambda = v/f = 600cm/50 = 12cm
k = -1 vào (*) ta được: d = 21cm
OM = \sqrt {{d^2} - {\rm{O}}{{\rm{S}}_1}^2} = \sqrt {{{21}^2} - {{15}^2}_{^{}}} = 216 = 6\sqrt 6 cm
Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp S1 và S2 cách nhau 20cm, dao động theo phương thẳng đứng với phương trình
u{\rm{ }} = {\rm{ }}2cos40\pi t{\rm{ }}\left( {mm} \right) . Biết tốc độ truyền sóng trên mặt chất lỏng là 40 cm/s. Phần tử O thuộc bề mặt chất lỏng là trung điểm của S1S2. Điểm trên mặt chất lỏng thuộc trung trực của S1S2 dao động cùng pha với O, gần O nhất, cách O đoạn:
\lambda = {\rm{ }}2cm
Cách 1:
Ta có:
{k_0} = \frac{{{S_1}{S_2}}}{{2\lambda }} = 5
=> O cùng pha nguồn.Vậy M cần tìm cùng pha nguồn
Phương trình sóng tổng hợp tại M là:
{u_M} = 2acos(\pi \frac{{{d_2} - {d_1}}}{\lambda })cos(20\pi t{\rm{ }} - \pi \frac{{{d_2} + {d_1}}}{\lambda })
Để M dao động cùng pha với S1, S2 thì:
\pi \frac{{{d_2} + {d_1}}}{\lambda } = 2k\pi ; Với d1 = d2 ta có: d1 = d2 = 2k;
Pytago :
{x^2} = {\left( {2k} \right)^2} - {10^2}
Đk có nghĩa:
\left| k \right|{\rm{ }} \ge {\rm{ }}5 chọn k{\rm{ }} = {\rm{ }}6 \to x = 2\sqrt {11} cm = 6,6cm
Cách 2:
Ta có:
{k_0} = \frac{{{S_1}{S_2}}}{{2\lambda }} = 5
=> O cùng pha nguồn.Vậy M cần tìm cùng pha nguồn
Chọn klàm tròn = 5 .Cùng pha gần nhất: chọn k = klàm tròn + 1 =6.
Ta tính:
d = k\lambda = 12
.Khoảng cách cần tìm:
OM{\rm{ }} = \sqrt {{d^2} - {{\left( {\frac{{S{}_1{S_2}}}{2}} \right)}^2}} = 2\sqrt {11} cm = 6,6cm
Hai nguồn sóng kết hợp, đặt tại A và B cách nhau 20 cm dao động theo phương trình u{\rm{ }} = {\rm{ }}acos\left( {\omega t} \right) trên mặt nước, coi biên độ không đổi, bước sóng \lambda = {\rm{ }}3{\rm{ }}cm . Gọi O là trung điểm của AB. Một điểm nằm trên đường trung trực AB, dao động cùng pha với các nguồn A và B, cách A hoặc B một đoạn nhỏ nhất là:
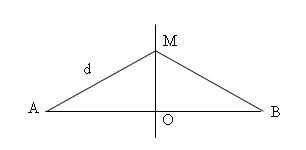
Biểu thức sóng tại A, B
u{\rm{ }} = {\rm{ }}acos\omega t
Xét điểm M trên trung trực của AB:
AM{\rm{ }} = {\rm{ }}BM{\rm{ }} = {\rm{ }}d{\rm{ }}\left( {cm} \right){\rm{ }} \ge {\rm{ }}10{\rm{ }}cm
Biểu thức sóng tại M:
{u_M} = {\rm{ }}2acos(\omega t - \frac{{2\pi d}}{\lambda })
Điểm M dao động cùng pha với nguồn khi:
\begin{array}{l}\frac{{2\pi d}}{\lambda } = 2k\pi \to d = k\lambda = 3k \ge 10 \to k \ge 4\\d = {d_{\min }} = 4.3 = 12cm\end{array}
Ở mặt chất lỏng có hai nguồn sóng A, B cách nhau 19 cm, dao động theo phương thẳng đứng với phương trình là {u_A} = {\rm{ }}{u_B} = {\rm{ }}acos20\pi t (với t tính bằng s). Tốc độ truyền sóng của mặt chất lỏng là 40 cm/s. Gọi M là điểm ở mặt chất lỏng gần A nhất sao cho phần tử chất lỏng tại M dao động với biên độ cực đại và cùng pha với nguồn A. Khoảng cách AM là:
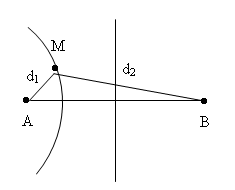
\lambda = \frac{v}{f} = 4cm
Cách 1:
Xét điểm M: AM = d1; BM = d2
\begin{array}{l}{u_M} = acos(20\pi t{\rm{ }} - \frac{{2\pi {d_1}}}{\lambda }) + {\rm{ }}acos(20\pi t - \frac{{2\pi {d_2}}}{\lambda })\\ = 2acos(\frac{{\pi ({d_2} - {d_1})}}{\lambda })cos(20\pi t - \frac{{\pi ({d_1} + {d_2})}}{\lambda })\end{array}
Điểm M dao động với biên độ cực đại, cùng pha với nguồn A khi:
cos(\frac{{\pi ({d_2} - {d_1})}}{\lambda }) = 1 và \frac{{\pi ({d_1} + {d_2})}}{\lambda } = 2k\pi
\to \left\{ \begin{array}{l}{d_2} - {d_1} = 2k'\lambda \\{d_2} + {d_1} = 2k\lambda \end{array} \right. \to {d_1} = \left| {k - k'} \right|\lambda
Điểm M gần A nhất ứng với k - k' = 1 \to {d_{1\min }} = \lambda = 4cm
Cách 2:
Số cực đại giao thoa:
- \frac{{AB}}{\lambda } \le k \le \frac{{AB}}{\lambda } \to k = - 4;\, - 3;......3;\,4.
Điểm M gần A nhất dao động với Amax ứng với k = 4 (hoặc -4).
Phương trình dao động tại điểm M là:
{u_M} = 2a\cos (\omega t - \frac{{\pi ({d_1} + {d_2})}}{\lambda }) .
Độ lệch pha dao động giữa nguồn A và M là:
\Delta \varphi = \frac{{\pi ({d_1} + {d_2})}}{\lambda }
Do M dao động cùng pha với nguồn A nên:
\Delta \varphi = \frac{{\pi ({d_1} + {d_2})}}{\lambda } = n.2\pi \to ({d_1} + {d_2}) = 2n\lambda = 8n\,(cm)(1)
Mặt khác:
{d_1} + {d_2} \ge AB = 19\,cm (2).
Từ (1) và (2) ta có: n \ge 2,375 Vậy n nhận các giá trị: 3, 4, 5……
Mặt khác: M dao động với biên độ cực đại nên:
{d_2} - {d_1} = 4\lambda = 16\,(cm) (3)
Từ (1), (2) và (3) ta được:
{d_1} = 4n - 8 \to {d_{1\min }} = 4.3 - 8 = 4\,(cm).
Dùng một âm thoa có tần số rung f = 100Hz người ta tạo ra hai điểm S1,S2 trên mặt nước hai nguồn sóng cùng biên độ,cùng pha.S1S2 = 3,2cm.Tốc độ truyền sóng là 40 cm/s. I là trung điểm của S1S2. Định những điểm dao động cùng pha với I.Tính khoảng từ I đến điểm M gần I nhất dao động cùng pha với I và nằm trên trung trực S1S2 là:
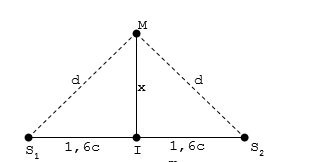
Ta có:
\lambda = \frac{v}{f} = 0,4cm
- Giả sử phương trình sóng của 2 nguồn là
{u_{S1}} = {\rm{ }}{u_{S2}} = {\rm{ }}Acos(200\pi t)
- Thì phương trình sóng tại I là:
{u_I} = {u_{1I}} + {u_{2I}} = 2A\cos (200\pi t - 2\pi \frac{{1,6}}{{0,4}}) = 2A\cos (200\pi t - 8\pi ) = 2A\cos (200\pi t)
-Tương tự PT sóng tại M cách mỗi nguồn đoạn d ( như hình vẽ ) là:
{u_M} = 2A\cos (200\pi t - 2\pi \frac{d}{{0,4}})
=> Độ lệch pha giữa I và M là
\Delta \varphi = 2\pi \frac{d}{{0,4}}
để I và M cùng pha thì
\Delta \varphi = k2\pi \to d = k.0,4(cm)
Theo hình vẽ dễ thấy
d > 1,6{\text{ }}cm \to d = k.0,4 > 1,6 \Rightarrow k > 4
* Mặt khác cần tìm xmin nên d cũng phải min => k cũng min => kmin=5 => dmin=5.0,4=2cm
{x_{min}} = \sqrt {d_{\min }^2 - 1,{6^2}} = 1,2cm
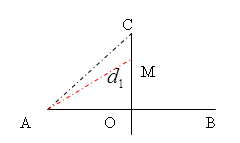
Ba điểm A, B, C trên mặt nước là 3 đỉnh của tam giác đều có cạnh bằng 8cm, trong đó A và B là 2 nguồn phát sóng giống nhau, có bước sóng 0,8cm. Điểm M trên đường trung trực của AB, dao động cùng pha với điểm C và gần C nhất thì phải cách C một khoảng bao nhiêu?
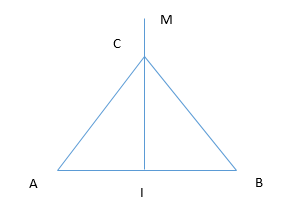
Ta có hai điểm M và C cùng pha:
\dfrac{{2\pi AC}}{\lambda } - \dfrac{{2\pi AM}}{\lambda } = 2k\pi
Suy ra:
AC{\rm{ }}-{\rm{ }}AM{\rm{ }} = \lambda
Xét điểm M nằm trong khoảng CO (O là trung điểm AB). Suy ra AM = AC - \lambda = 8 - 0,8
CM{\rm{ }} = {\rm{ }}CO{\rm{ }}-{\rm{ }}MO{\rm{ }} = \sqrt {A{C^2} - A{O^2}} - \sqrt {A{M^2} - A{O^2}} (với AC = 8 cm, AO = 4cm)
Suy ra CM = 0,94 cm (loại)
Xét điểm M nằm ngoài đoạn CO.
Suy ra:
AM{\rm{ }} = {\rm{ }}AC{\rm{ }} + \lambda = {\rm{ }}8{\rm{ }} + {\rm{ }}0,8
CM{\rm{ }} = {\rm{ }}MO{\rm{ }}-{\rm{ }}CO{\rm{ }} = \sqrt {A{M^2} - A{O^2}} - \sqrt {A{C^2} - A{O^2}} (với AC = 8 cm, AO = 4cm).
Suy ra CM = 0,91cm (nhận)
Vậy khoảng cách ngắn nhất giữa M và C dao động cùng pha là 0,91 cm.
Trên mặt nước có 2 nguồn sóng giống hệt nhau A và B cách nhau một khoảng AB = 24cm. Bước sóng \lambda = {\rm{ }}2,5{\rm{ }}cm. Hai điểm M và N trên mặt nước cùng cách đều trung điểm của đoạn AB một đoạn 16 cm và cùng cách đều 2 nguồn sóng và A và B. Số điểm trên đoạn MN dao động cùng pha với 2 nguồn là:
Cách 1: Gọi M là điểm dao động cùng pha với nguồn
Phương trình sóng tổng hợp tại M là:
u_M= 2acos(π \dfrac{{{d_2} - {d_1}}}{\lambda })cos(20πt - π\dfrac{{{d_2} + {d_1}}}{\lambda })
Để M dao động cùng pha với S1 thì:
π\dfrac{{{d_2} + {d_1}}}{\lambda } = 2kπ
suy ra: {d_2} + {d_1} = 2k\lambda
Với d1 = d2 ta có:
{d_2} = {d_1} = k\lambda
Gọi x là khoảng cách từ M đến AB:
{d_1} = {\rm{ }}{d_2} = \sqrt {{x^2} + {{\left( {\dfrac{{AB}}{2}} \right)}^2}} = k\lambda
Suy ra
\left| x \right| = \sqrt {{{\left( {k\lambda } \right)}^2} - {{\left( {\dfrac{{AB}}{2}} \right)}^2}} \\= \sqrt {6,25{k^2} - 144}
Với
0 \le x \le 16 \leftrightarrow 4,8 \le k \le 8 \\\leftrightarrow k{\rm{ }} = {\rm{ }}5,{\rm{ }}6,{\rm{ }}7,{\rm{ }}8.
Vậy trên đoạn MN có 2 x 4 = 8 điểm dao động cùng pha với hai nguồn.
Cách 2: \lambda = 2,5cm;{k_0} = \dfrac{{{S_1}{S_2}}}{{2\lambda }} = 4,8
{d_M} = \sqrt {O{M^2} + {{\left( {\dfrac{{{S_1}{S_2}}}{2}} \right)}^2}} {d_N} \\= \sqrt {O{N^2} + {{\left( {\dfrac{{{S_1}{S_2}}}{2}} \right)}^2}} = 20cm \\\to {k_M} = \dfrac{{{d_M}}}{\lambda } = 8
chọn 5, 6, 7, 8
{d_N} = \sqrt {O{N^2} + {{\left( {\dfrac{{{S_1}{S_2}}}{2}} \right)}^2}} = 20cm \\\to {k_N} = \dfrac{{{d_N}}}{\lambda } = 8
chọn 5,6,7,8 M, N ở 2 phía vậy có 4 + 4 = 8 điểm
Có hai nguồn sóng cơ kết hợp A và B trên mặt nước cách nhau một đoạn AB = 9\lambda phát ra dao động với phương trình u{\rm{ }} = {\rm{ }}acos\omega t . Xác định trên đoạn AB, số điểm có biên độ cực đại cùng pha với nhau và cùng pha với nguồn, không kể hai nguồn là bao nhiêu?
Cách 1:
Xét điểm M trên S1S2
S1M = d1; S2M = d2. Ta có:
{u_{1M}} = acos(\omega t - \frac{{2\pi {d_1}}}{\lambda });{u_{2M}} = acos(\omega t - \frac{{2\pi {d_2}}}{\lambda })
{u_M} = {u_{1M}} + {u_{2M}} = 2cos(\frac{{\pi ({d_2} - {d_1})}}{\lambda })cos(\omega t - \frac{{\pi ({d_1} + {d_2})}}{\lambda }) = 2acos\frac{{\pi ({d_2} - {d_1})}}{\lambda }cos(\omega t{\rm{ }} - 9\pi )
Để M là điểm dao động với biên độ cực đại, cùng pha với nguồn thì
cos\frac{{\pi ({d_2} - {d_1})}}{\lambda }= - 1
\to \frac{{\pi ({d_2} - {d_1})}}{\lambda } = {\text{ }}\left( {2k{\text{ }} + {\text{ }}1} \right)\pi \to {d_2}--{\text{ }}{d_1} = {\text{ }}\left( {2k{\text{ }} + {\text{ }}1} \right)\lambda \left( 1 \right)
Và ta có:
{d_1} + {\text{ }}{d_2} = {\text{ }}9\lambda \left( 2 \right)
Từ (1) và (2)
= > {d_1} = {\text{ }}\left( {4{\text{ }} - {\text{ }}k} \right)\lambda
Ta có:
0{\text{ }} < {\text{ }}{d_1} = {\text{ }}\left( {4{\text{ }} - {\text{ }}k} \right)\lambda {\text{ }} < {\text{ }}9\lambda {\text{ }} = > - {\text{ }}5{\text{ }} < {\text{ }}k{\text{ }} < {\text{ }}4 = > - {\text{ }}4 \leqslant k \leqslant {\text{ }}3{\text{ }}.
Do đó có 8 giá trị của k

Cách 2: Vì hai nguồn đồng pha nên trung điểm 0 của AB là một cực đại
Dễ dàng tính được số cực đại (không kể hai nguồn) trên AB:
{N_{c{\text{d}}}} = 2\left[ {\dfrac{L}{\lambda }} \right] + 1 - 2 = 17
Vậy: Ở mỗi bên 0 có 8 cực đại
Mặt khác chứng minh được dao động tại 0 có phương trình:
{u_0} = 2A\cos (\omega t - \frac{d}{\lambda }2\pi ) = 2A\cos (\omega t - \frac{1}{{2\lambda }}2\pi ) = 2A\cos (\omega t - 9\pi )
, tức 0 là cực đại ngược pha với nguồn
Sử dụng sự tương tự với hiện tượng sóng dừng sẽ thấy các cực đại thứ 1, 3, 5, 7 ở mỗi bên sẽ ngược pha với O hay đồng pha với nguồn.
=> 8 điểm
Trên mặt nước có hai nguồn kết hợp AB cùng pha cách nhau một đoạn 12cm đang dao động vuông góc với mặt nước tạo ra sóng với bước sóng 1,6cm. Gọi C là một điểm trên mặt nước cách đều hai nguồn và cách trung điểm O của đoạn AB một khoản 8cm. Hỏi trên đoạn CO, số điểm dao động cùng pha với nguồn là:
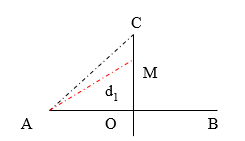
+ Do hai nguồn dao động cùng pha nên để đơn giản ta cho pha ban đầu của chúng bằng 0.
+ Độ lệch pha giữa hai điểm trên phương truyền sóng:
\Delta \varphi = \dfrac{{2\pi d}}{\lambda }.
+ Xét điểm M trên đường trung trực của AB cách A một đoạn d1 và cách B một đoạn d2. Suy ra d1=d2.
+ Mặt khác điểm M dao động cùng pha với nguồn nên
\Delta \varphi = \dfrac{{2\pi {d_1}}}{\lambda } = k2\pi \to {d_1} = k\lambda = 1,6k(1).
+ Mà :
AO \le {d_1} \le AC \to \dfrac{{AB}}{2} \le 1,6k \le \sqrt {{{\left( {\dfrac{{AB}}{2}} \right)}^2} + O{C^2}}
(Do AO = \dfrac{{AB}}{2} và AC = \sqrt {{{\left( {\dfrac{{AB}}{2}} \right)}^2} + O{C^2}} = 10(cm))
\Rightarrow 6 \le 1,6k \le 10 \Rightarrow 3,75 \le k \le 6,25 \Rightarrow k = 4;5;6
=> Trên đoạn CO có 3 điểm dao dộng cùng pha với nguồn.
Trên mặt nước có hai nguồn sóng giống nhau A và B, cách nhau khoảng AB = 12(cm) đang dao động vuông góc với mặt nước tạo ra sóng có bước sóng \lambda = {\rm{ }}1,6cm . C và D là hai điểm khác nhau trên mặt nước, cách đều hai nguồn và cách trung điểm O của AB một khoảng 8(cm). Số điểm dao động cùng pha với nguồn ở trên đoạn CD là
Cách 1:
Tính trên CD:
AO \leqslant {d_2} - {\text{ }}{d_1} = k\lambda \leqslant AC
\Leftrightarrow \frac{6}{{1,6}} < k < \frac{{1,0}}{{1,6}} \Leftrightarrow k = 4,5,6
Þ Có tất cả 6 giá trị k thoả mãn
Cách 2: Phương trình tổng hợp tại 1 điểm trên OD:
u = 2a\cos (2\pi ft - \pi \frac{{2d}}{\lambda })
Cùng pha=>
\pi \frac{{2d}}{\lambda } = 2k\pi \Rightarrow d = 1,6\lambda có 6 \le d = 1,6k \le 10 \Rightarrow k = 4;5;6 do tính đối xứng nên có 6 điểm
Ba điểm A, B, C trên mặt nước là ba đỉnh của tam giac đều có cạnh 16 cm trong đó A và B là hai nguồn phát sóng có phương trình {u_1} = {u_2} = 2\cos (20\pi t)(cm),sóng truyền trên mặt nước không suy giảm và có vận tốc 20 (cm/s).M trung điểm của AB .Số điểm dao động cùng pha với điểm C trên đoạn MC là:
+ Bước sóng :
\lambda = \frac{v}{f} = 2(cm)
+ Gọi N là điểm nằm trên đoạn MC cách A và B một khoảng d với
AB/2{\rm{ }} = {\rm{ }}8\left( {cm} \right)d{\rm{ }} < {\rm{ }}AC{\rm{ }} = {\rm{ }}16\left( {cm} \right) .
+ Phương trình sóng tổng hợp tại N :
{u_N} = 4\cos (20\pi t - \frac{{2\pi d}}{\lambda }) = 4\cos (20\pi t - \pi d)(cm)
+ Phương trình sóng tổng hợp tại C :
{u_C} = 4\cos (20\pi t - \frac{{2\pi AC}}{\lambda }) = 4\cos (20\pi t - 16\pi )(cm)
+ Điểm N dao động cùng pha với C :
\Rightarrow \pi d - 16\pi = k2\pi (k \in Z) \Rightarrow d = 16 + 2k(cm) \Rightarrow 8 \le 16 + 2k < 16
\Rightarrow \left\{ \begin{array}{l} - 4 \le k < 0\\k \in Z\end{array} \right. \Rightarrow k = - 4, - 3, - 2, - 1 \Rightarrow
Có 4 điểm dao động cùng pha với C.
Hai nguồn phát sóng kết hợp A và B trên mặt chất lỏng dao động theo phương trình:
{u_A} = {\rm{ }}acos(100\pi t);{\rm{ }}{u_B} = {\rm{ }}bcos(100\pi t) . Tốc độ truyền sóng trên mặt chất lỏng 1m/s. I là trung điểm của AB. M là điểm nằm trên đoạn AI, N là điểm nằm trên đoạn IB. Biết IM = 5 cm và IN = 6,5 cm. Số điểm nằm trên đoạn MN có biên độ cực đại và cùng pha với I là:

Hai nguồn cùng pha, trung điểm I dao động cực đại
Những điểm dao động cùng pha với I cách I một số nguyên lần bước sóng
IM{\rm{ }} = {\rm{ }}5cm{\rm{ }} = {\rm{ }}2,5\lambda nên có 2 điểm
IN{\rm{ }} = {\rm{ }}6,5cm{\rm{ }} = {\rm{ }}3,25\lambda nên có 3 điểm
Tổng số điểm dao động cùng pha với I trên MN là 5
Hai mũi nhọn A, B cách nhau 8 cm gắn vào đầu một cần rung có tần số f = 100 Hz, đặt chạm nhẹ vào mặt một chất lỏng. Tốc độ truyền sóng trên mặt chất lỏng v = 0,8 m/s. Hai nguồn A, B dao động theo phương thẳng đứng với cùng phương trình {u_A} = {\rm{ }}{u_B} = {\rm{ }}acos(\omega t){\rm{ }}cm. Một điểm M trên mặt chất lỏng cách đều A, B một khoảng d = 8 cm. Tìm trên đường trung trực của AB hai điểm M1,M2 gần M nhất và dao động cùng pha với M.
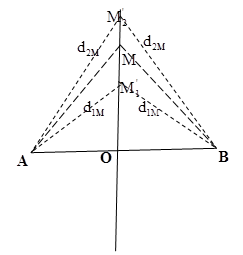
Ta có:
+ Bước sóng: \lambda = \dfrac{v}{f} = \dfrac{{0,8}}{{100}} = {8.10^{ - 3}}m = 0,8cm
+ Ta có phương trình giao thoa sóng trên đường trung trực của S1S2 là:
u = 2Ac{\rm{os}}\left( {\dfrac{\pi }{\lambda }\left( {{d_1} - {d_2}} \right)} \right){\rm{cos}}\left( {\omega t - \dfrac{\pi }{\lambda }\left( {{d_1} + {d_2}} \right)} \right)
theo giả thuyết hai sóng cùng pha trên đường trung trực nên ta có:
\left( {\dfrac{\pi }{\lambda }\left( {{d_{1M}} + {d_{2M}}} \right) - \dfrac{\pi }{\lambda }\left( {{d_{1{M_1}}} + {d_{2{M_1}}}} \right)} \right) = 2k\pi {\rm{ (1}})
mà
{d_{1M}} = {\rm{ }}{d_{2M}} = {\rm{ }}{d_M} = {\rm{ }}8{\rm{ }}cm
{d_{1M1}} = {\rm{ }}{d_{2M1}} = {\rm{ }}{d_{M1}}
từ (1) suy ra
{d_M}-{\rm{ }}{d_{M1}} = {\rm{ }}\lambda {\rm{ }}\left( {{\rm{ }}\lambda = {\rm{ }}0,8/100{\rm{ }} = {\rm{ }}0,8{\rm{ }}cm} \right)
{d_{M1}} = {\rm{ }}{d_M}-{\rm{ }}\lambda {\rm{ }} = {\rm{ }}8{\rm{ }}-{\rm{ }}0,8{\rm{ }} = {\rm{ }}7,2{\rm{ }}\left( {cm} \right)
suy ra:
O{M_1} = \sqrt {d_{{M_1}}^2 - O{A^2}} = \sqrt {7,{2^2} - {4^2}} = 5,99cm
{d_{M2}} = {\rm{ }}{d_M} + {\rm{ }}\lambda {\rm{ }} = {\rm{ }}8{\rm{ }} + {\rm{ }}0,8{\rm{ }} = {\rm{ }}8,8{\rm{ }}\left( {cm} \right)
suy ra:
O{M_2} = \sqrt {d_{{M_2}}^2 - O{A^2}} = \sqrt {8,{8^2} - {4^2}} = 7,84cm
mà
OM = \sqrt {d_1^2 - O{A^2}} = \sqrt {{8^2} - {4^2}} = 6,93cm
vậy:
M{M_1} = OM - O{M_1} = 0,94cm \to {M_2}M = O{M_2} - OM = 0,91cm
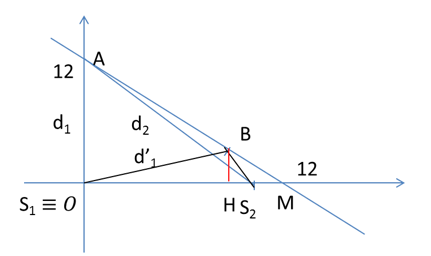
Trong thí nghiệm giao thoa sóng mặt nước, 2 nguồn sóng S1 và S2 cách nhau 11cm và dao động điều hòa theo phương vuông góc với mặt nước có cùng phương trình {u_1} = {u_2} = 5c{\rm{os}}\left( {50\pi t} \right)mm . Tốc độ truyền sóng v = 0,5 m/s và biên độ sóng không đổi khi truyền đi. Chọn hệ trục xOy thuộc mặt phẳng mặt nước khi yên lặng, gốc O trùng với S1, Ox trùng S1S2. Trong không gian, phía trên mặt nước có 1 chất điểm chuyển động mà hình chiếu (P) của nó với mặt nước chuyển động với phương trình y = 12 - x và có tốc độ {v_1} = 5\sqrt 2 cm/s. Trong thời gian t = 2 (s) kể từ lúc (P) có tọa độ x = 0 thì (P) cắt bao nhiêu vân cực tiểu trong vùng giao thoa của sóng?
Ta có:
\lambda = \dfrac{v}{f} = \dfrac{v}{{\dfrac{\omega }{{2\pi }}}} = \dfrac{{0,5}}{{\dfrac{{50}}{{2\pi }}}} = 0,02m = 2cm
Trong không gian có một chất điểm dao động mà hình chiếu của nó lên mặt nước là đường thẳng y = 12 - x.
Vận tốc chuyển động là: {v_1} = 5\sqrt 2 cm/s
Sau 2s, quãng đường mà vật đi được là: S = AB = {v_1}t = 10\sqrt 2 cm
Tại B cách S1, S2 những khoảng d’1, d’2.
Gọi H - hình chiếu của B trên S1S2
S2M = 1cm
HM = 2cm = HB
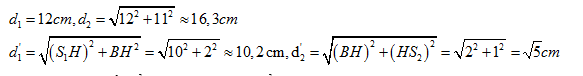
Trên đoạn BM số điểm có biên độ cực tiểu thỏa mãn:
\begin{array}{l}d{'_2} - d{'_1} \le (k + \dfrac{1}{2})\lambda \le {d_2} - {d_1}\\ \leftrightarrow - 4,48 \le k \le 1,65\\ \to k = - 4, - 3, - 2, - 1,0,1\end{array}.
=> Có 6 điểm
Trên mặt nước có hai nguồn kết hợp dao động theo phương vuông góc mặt nước tại hai điểm S1 và S2 với các phương trình lần lượt là: {u_1} = a.\cos \left( {10\pi t} \right)cmvà {u_2} = a.\cos \left( {10\pi t + \dfrac{\pi }{2}} \right)cm. Biết tốc độ truyền sóng trên mặt nước là 1m/s. Hai điểm M và N thuộc vùng hai sóng giao thoa, biết M{S_1}-M{S_2} = 5cmvà N{S_1}-N{S_2} = 35cm. Chọn phát biểu đúng?
Bước sóng :
\lambda = v.T = v.\dfrac{{2\pi }}{\omega } = 100.\dfrac{{2\pi }}{{10\pi }} = 20cm
Độ lệch pha của hai sóng truyền tới M :
\Delta \varphi = \dfrac{{2\pi \left( {{d_1} - {d_2}} \right)}}{\lambda } + \dfrac{\pi }{2} = \dfrac{{2\pi .5}}{{20}} + \dfrac{\pi }{2} = \pi
Vậy M thuộc cực tiểu giao thoa
Độ lệch pha của hai sóng truyền tới N là:
\Delta \varphi = \dfrac{{2\pi \left( {{d_1} - {d_2}} \right)}}{\lambda } + \dfrac{\pi }{2} = \dfrac{{2\pi .35}}{{20}} + \dfrac{\pi }{2} = 4\pi
Vậy N thuộc cực đại giao thoa
Trong thí nghiệm giao thoa sóng mặt nước giữa hai nguồn đồng bộ tần số 25Hz , cách nhau S1S2=32 cm , tốc độ truyền sóng trên mặt nước là 30 cm/s. M là điểm trên mặt nước cách đều hai nguồn S1, S2 và cách trung điểm I của S1S2 một khoảng 12 cm . Số điểm dao động cùng pha với hai nguồn nằm trong đoạn thẳng MI là
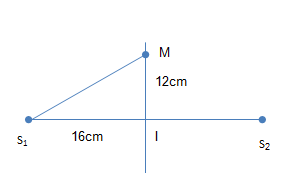
Hai nguồn đồng bộ dao động với phương trìnhu=Ac\text{os(}\omega \text{t+}\varphi )
Gọi điểm N cách hai nguồn khoảng d, N thuộc đoạn MI. Phương trình dao động sóng tại N:{{u}_{N}}=2Ac\text{os(}\omega \text{t-}\frac{2\pi d}{\lambda }+\varphi )
Độ lệch pha giữa hai điểm N và nguồn là: \Delta \varphi =\frac{2\pi d}{\lambda }
Để N dao động cùng pha với nguồn: \Delta \varphi =k.2\pi \to \frac{2\pi d}{\lambda }=k.2\pi \to d=k\lambda =k.\frac{v}{f}=1,2.k(cm)
Vì N thuộc đoạn MI: {{S}_{1}}I\le {{S}_{1}}N\le {{S}_{1}}M\to 16\le 1,2.k\le \sqrt{{{16}^{2}}+{{12}^{2}}}\to 13,3\le k\le 16,6
ð Có 3 giá trị của k
Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn S1, S2 cách nhau 20cm dao động theo phương thẳng đứng với các phương trình u1 = u2 = Acos(ωt). Bước sóng trên mặt nước do hai nguồn này tạo ra là 4cm. Trên mặt nước, xét một vân giao thoa cực đại gần đường trung trực của S1S2 nhất. Số điểm dao động cùng pha với S1, S2 nằm trên vân này và thuộc hình tròn đường kính S1S2 là
Xét tại điểm M và N đều nằm trên cực đại giao thoa gần trung trực nhất với M nằm trên đường kính S1S2 và N nằm trên đường tròn đường kính S1S2
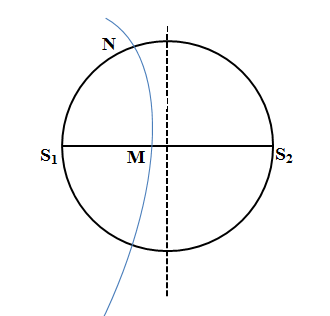
MS2 – MS1 = λ = 4cm
MS2 + MS1 = S1S2 = 20cm
=> MS2 = 12cm, MS1 = 8cm
NS2 – NS1 = 4cm
ΔNS1S2 vuông tại N nên NS_{2}^{2}+NS_{1}^{2}={{S}_{1}}{{S}_{2}}^{2}={{20}^{2}}
=> NS1 = 12cm, NS2= 16cm
Xét trên đoạn MN, số điểm dao động cùng pha với nguồn phải thỏa mãn:
\frac{\pi ({{d}_{1}}+{{d}_{2}})}{\lambda }=2k\pi \Rightarrow M{{S}_{1}}+M{{S}_{2}}\le {{d}_{1}}+{{d}_{2}}=2k\lambda \le N{{S}_{1}}+N{{S}_{2}}
=> 20 ≤ 8k ≤ 28 => 2,5≤ k ≤ 3,5 => có 1 giá trị k nguyên ứng với 1 điểm cùng pha với hai nguồn
Vậy trên hai nửa hypebol có 2 điểm dao động cùng pha với hai nguồn.
Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng . Hai điểm M và N thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước dao động.Biết OM= 8λ; ON =12λ và OM vuông góc ON.Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là
Gọi I là điểm bất kỳ nằm trên MN.
Độ lệch pha dao động giữa nguồn và I là \Delta \varphi =\frac{2\pi d}{\lambda }=(2k+1)\pi \Rightarrow d=(2k+1)\frac{\lambda }{2}
Gọi H là trung điểm của MN, khi đó OH=\frac{MN}{2}=2\sqrt{13}\lambda
Số điểm dao động ngược pha với O trên đoạn NH là
2\sqrt{13}\lambda \le (2k+1)\frac{\lambda }{2}\le 12\lambda \Rightarrow 6,7\le k\le 12,5
=> Có 5 điểm
Số điểm dao động ngược pha với O trên đoạn MH là:
2\sqrt{13}\lambda \le (2k+1)\frac{\lambda }{2}\le 8\lambda \Rightarrow 6,7\le k\le 7,5
=> Có 1 điểm
Vậy có tất cả 6 điểm dao động ngược pha với O trên đoạn MN

