Bài tập mạch xoay chiều RLC - có R thay đổi

\({U_C} = I{Z_C} = \dfrac{U}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}{Z_C}\)

\({U_{Cm{\rm{ax}}}} \leftrightarrow {Z_{\min }} \to \) R tiến về 0

Hiệu điện thế 2 đầu điện trở: \({U_R} = \dfrac{U}{{\sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} }}{\rm{R = }}\dfrac{U}{{\sqrt {1 + \dfrac{{{{({Z_L} - {Z_C})}^2}}}{{{R^2}}}} }}\)

Khi đó \({U_R}Max\)  <=>  \(1 + \dfrac{{{{({Z_L} - {Z_C})}^2}}}{{{R^2}}}\)Min

<=>  R tiến về vô cùng

\(P = UIc{\rm{os}}\varphi {\rm{ = }}{{\rm{I}}^2}R = \dfrac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R = \dfrac{{{U^2}}}{{R + \dfrac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}}}\)

Để P_max \( \to {\left( {R + \dfrac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}} \right)_{\min }}\)

Ta có: \(R + \dfrac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R} \ge 2\sqrt {R\dfrac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}}  = 2\left| {{Z_L} - {Z_C}} \right|\)

Dấu “=” xảy ra \( \leftrightarrow {R^2} = {({Z_L} - {Z_C})^2} \to R = \left| {{Z_L} - {Z_C}} \right|\)

Mạch chỉ có điện trở R

+ Khi đặt hiệu điện thế xoay chiều thì công suất tiêu thụ trên R là: \(P = {I^2}R = \dfrac{{{U^2}}}{R}\)

+ Khi đặt hiệu điện thế không đổi thì công suất tiêu thụ trên R là : \(P' = \dfrac{{{U^2}}}{R}\)

\( \to P' = P\)

\({Z_C} = 100\Omega \)

Khi điều chỉnh R có 2 giá trị \({R_1},{R_2}\) mạch có cùng công suất tiêu thụ, ta được:

\({R_1}{R_2} = Z_C^2\) (1)

Mặt khác, theo đầu bài, ta có:

\(\begin{array}{l}{U_{{C_1}}} = 2{U_{{C_2}}}\\ \leftrightarrow {I_1}{Z_C} = 2{I_2}{Z_C}\\ \to {I_1} = 2{I_2}\\ \leftrightarrow \dfrac{U}{{\sqrt {R_1^2 + Z_C^2} }} = 2\dfrac{U}{{\sqrt {R_2^2 + Z_C^2} }}\end{array}\)

\( \to R_2^2 + Z_C^2 = 4\left( {R_1^2 + Z_C^2} \right)\)  (2)

Từ (1) và (2) ta suy ra:

\(R_2^2 - 4R_1^2 = 3Z_C^2 = 3{R_1}{R_2}\)

Với \({R_1} \ne 0\), chia cả hai vế cho \(R_1^2\), ta được:

\(\begin{array}{l}\dfrac{{R_2^2}}{{R_1^2}} - 3\dfrac{{{R_2}}}{{{R_1}}} - 4 = 0\\ \to \left[ \begin{array}{l}{R_2} = 4{R_1}\\{R_2} =  - {R_1}(loai)\end{array} \right.\end{array}\)

Với \({R_2} = 4{R_1}\)  thay vào (1) ta suy ra: \(\left\{ \begin{array}{l}{R_1} = 50\Omega \\{R_2} = 200\Omega \end{array} \right.\)

+ Khi  \(R = {R_0},{P_{\max }} \to {R_0} = \left| {{Z_L} - {Z_C}} \right|\)

+ Khi  \({R_1} = {R_0} + 15\) và  \({R_2} = {R_0} - 5\)  thì có cùng \({P_0}\)

\(\begin{array}{l} \to {R_1}{R_2} = {\left( {{Z_L} - {Z_C}} \right)^2} = {R_{Pm{\rm{ax}}}}^2 = {R_0}^2\\ \leftrightarrow ({R_0} + 15)({R_0} - 5) = {R_0}^2\\ \to {R_0} = 7,5\Omega \end{array}\)

Ta có:

\(\begin{array}{l}U = U_{R1}^2 + U_{C1}^2 = U_{R2}^2 + U_{C2}^2\\ \to U_{R1}^2 + U_{C1}^2 = 2U_{R1}^2 + \dfrac{{2U_{C1}^2}}{3}\\ \to \dfrac{{U_{C1}^2}}{3} = U_{R1}^2\\ \to {U_{C1}} = \sqrt 3 {U_{R1}}\end{array}\)

Khi đó: \(U = \sqrt {U_{R1}^2 + U_{C1}^2}  = \sqrt {U_{R1}^2 + 3U_{R1}^2}  = 2{U_{R1}}\)

Ta có: \(\left\{ \begin{array}{l}{\rm{cos}}{\varphi _1} = \dfrac{{{U_{{R_1}}}}}{U} = \dfrac{{{U_{{R_1}}}}}{{2{U_{{R_1}}}}} = \dfrac{1}{2}\\{\rm{cos}}{\varphi _2} = \dfrac{{{U_{{R_2}}}}}{U} = \dfrac{{\sqrt{2}{U_{{R_1}}}}}{{2{U_{{R_1}}}}} = \dfrac{1}{\sqrt{2}}\end{array} \right.\) 

Ta có:

+ Cảm kháng: \({Z_L} = {\rm{ }}\omega L = 100\pi .\dfrac{3}{{5\pi }} = 60\Omega \)

Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)

Hiệu điện thế hiệu dụng: \(U = {\rm{ }}100\sqrt 2 V\)

+ Công suất tiêu thụ của mạch là:

\(\begin{array}{l}P = \dfrac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R = \dfrac{{{U^2}}}{{{R^2} + {{40}^2}}}R\\ \leftrightarrow 240 = \dfrac{{{{\left( {100\sqrt 2 } \right)}^2}}}{{{R^2} + {{40}^2}}}R \to \left[ \begin{array}{l}R = 30\Omega \\R = \dfrac{{160}}{3}\Omega \end{array} \right.\end{array}\)

+ Cảm kháng của mạch: \({Z_L} = \omega L = 2\pi f.L = 2\pi .50.\dfrac{1}{\pi } = 100\Omega \)

+ Vì có 2 giá trị của R làm công suất của mạch bằng nhau nên \({R_1}.{R_2} = {\rm{ }}{Z_L}^2 = {100^2} = {10^4}\)

Điều chỉnh R thấy có 2 giá trị \({R_1},{\rm{ }}{R_2}\) mạch tiêu thụ cùng 1 công suất P

\(\begin{array}{l}{R_1} + {R_2} = \dfrac{{{U^2}}}{P}\\ \to P = \dfrac{{{U^2}}}{{{R_1} + {R_2}}} = \dfrac{{{{120}^2}}}{{40 + 20}} = 240W\end{array}\)

Ta có :

+ Tần số góc riêng của mạch: \({\omega _0} = \dfrac{1}{{\sqrt {LC} }}\)

=> tần số riêng của mạch: \(f = \dfrac{{{\omega _0}}}{{2\pi }} = \dfrac{1}{{2\pi \sqrt {LC} }}\)

+ Hiệu điện thế hiệu dụng \({U_{RL}}\)

\({U_{RL}} = I.{Z_{RL}} = \dfrac{{U\sqrt {{R^2} + Z_L^2} }}{{\sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{U}{{\sqrt {1 + \dfrac{{Z_C^2 - 2{Z_L}{Z_C}}}{{{R^2} + Z_L^2}}} }}\)

\({U_{RL}}\)  không phụ thuộc vào R   \( \leftrightarrow {Z_C} = 2{Z_L} \to \omega  = \dfrac{1}{{\sqrt {2LC} }}\)

=> Tần số \(f = \dfrac{\omega }{{2\pi }} = \dfrac{1}{{2\pi \sqrt {2LC} }} = \dfrac{{{f_0}}}{{\sqrt 2 }}\)

Vì có 2 giá trị \({R_1},{\rm{ }}{R_2}\) cho cùng công suất

Nên theo vi- et ta có:

\({R_1} + {\rm{ }}{R_2} = \dfrac{{{U^2}}}{P}\)

\( \to P = \frac{{{U^2}}}{{\left( {{R_1} + {R_2}} \right)}} = \frac{{{{220}^2}}}{{100}} = 484W\)

Ta có:

\({U_{AN}} = {U_{RL}} = \frac{U}{{\sqrt {\left( {{R^2} + {{\left( {{Z_L}{Z_c}} \right)}^2}} \right)} }}\sqrt {\left( {{R^2} + Z_L^2} \right)}  = \frac{U}{{\sqrt {\frac{{1 + \left( {Z_C^2 - 2{Z_C}{Z_L}} \right)}}{{{R^2} + Z_L^2}}} }}\)

Khi  đó điện áp hiệu dụng  giữa 2 đầu đoạn mạch AN không phụ thuộc vào R

\( \to {Z_C} = 2{Z_L} \to \omega  = \frac{1}{{\sqrt {2LC} }} \to \omega  = \frac{{{\omega _1}}}{{2\sqrt 2 }}\)

Khi điều chỉnh R thấy có 2 giá trị \({R_1},{\rm{ }}{R_2}\) mạch tiêu thụ cùng công suất

Nên theo vi- et ta có: \({R_1} + {R_2} = \frac{{{U^2}}}{P}\)

\( \to U = \sqrt {P({R_1} + {R_2})}  = \sqrt {36(60 + 84)}  = 72(V)\)

Khi điều chỉnh R thấy có 2 giá trị \({R_1},{\rm{ }}{R_2}\) mạch tiêu thụ cùng công suất

Nên theo vi- et ta có:

\(\begin{array}{l}{R_1}{R_2} = {\left( {{Z_L} - {Z_C}} \right)^2} = {R_{Pm{\rm{ax}}}}^2 = R_0^2\\ \to {R_0} = \sqrt {{R_1}{R_2}}  = \sqrt {36.64}  = 48\Omega \end{array}\)

Khi điều chỉnh R thấy có 2 giá trị \({R_1},{\rm{ }}{R_2}\) mạch tiêu thụ cùng công suất

Nên theo vi- et ta có:

\(\begin{array}{l}{R_1}{R_2} = {\left( {{Z_L} - {Z_C}} \right)^2} = {R_{Pm{\rm{ax}}}}^2 = R_0^2\\ \to {R_0} = \sqrt {{R_1}{R_2}}  = \sqrt {8.32}  = 16\Omega \end{array}\)

Khi đó công suất cực đại  \(P = \frac{{{U^2}}}{{2{R_0}}} = \frac{{{{120}^2}}}{{2.16}} = 450W\)

Ta có:

+ Khi  \(R = {R_0}\), công suất của mạch đạt cực đại \({P_{max}} = \dfrac{{{U^2}}}{{2{R_0}}}\)  (1) và khi đó \({R_0} = {Z_L}\) (theo BĐT cosi)

+ Khi \(R' = 3{R_0}\)

Ta có công suất: \(P = \dfrac{{{U^2}}}{{Z{'^2}}}R' = \dfrac{{{U^2}}}{{\left( {R{'^2} + Z_L^2} \right)}}R' = \dfrac{{{U^2}}}{{9R_0^2 + R_0^2}}3{R_0} = \dfrac{{3{U^2}}}{{10{R_0}}}\) (2)

Từ (1) và (2), ta suy ra: \(P = \dfrac{{3{P_{max}}}}{5} = 0,6{P_{max}}\)

+ Ta có:

- Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{\pi } = 100\Omega \)

- Dung kháng: \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{2.10}^{ - 4}}}}{\pi }}} = 50\Omega \)

Hiệu điện thế hiệu dụng: \(U = 220V\)

+ Công suất của mạch là: \(P = \dfrac{{{U^2}}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}R = \dfrac{{{U^2}}}{{R + \dfrac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}}}\)

Để \({P_{max}}\) thì  \(R + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R}\) phải min

Khi đó \(R = \left| {{Z_L} - {Z_C}} \right| = 100 - 50 = 50\Omega \)

\( \to {P_{max}} = \dfrac{{{U^2}}}{{2R}} = \dfrac{{{{220}^2}}}{{2.50}} = 484W\)

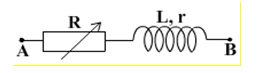
+ Hiệu điện thế hiệu dụng: \(U = \dfrac{{160}}{{\sqrt 2 }} = 80\sqrt 2 V\)

+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{{5\pi }} = 20\Omega \)

+ Công suất tiêu thụ trên mạch \({P_{max}}\) khi \(R + r = \left| {{Z_L} - {Z_C}} \right| = {Z_L} = 20\Omega \)

Khi đó, \({P_{max}} = \dfrac{{{U^2}}}{{2\left( {R + r} \right)}} = \dfrac{{{{\left( {80\sqrt 2 } \right)}^2}}}{{2.20}} = 320W\)

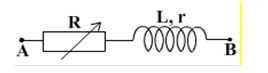
+ Hiệu điện thế hiệu dụng: \(U = \dfrac{{160}}{{\sqrt 2 }} = 80\sqrt 2 V\)

+ Cảm kháng: \({Z_L} = \omega L = 100\pi .\dfrac{1}{{5\pi }} = 20\Omega \)

+ Công suất tiêu thụ trên R max khi:

\(\begin{array}{l}{R^2} = {r^2} + {\left( {{Z_L} - {Z_C}} \right)^2}\\ \to R = \sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}  = \sqrt {{{15}^2} + {{\left( {20} \right)}^2}}  = 25\Omega \end{array}\)

Công suất cực đại khi đó:

\({P_{{\rm{max}}}} = \dfrac{{{U^2}}}{{2{\rm{r}} + 2\sqrt {{r^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }} = \dfrac{{{{(80\sqrt 2 )}^2}}}{{2.15 + 2\sqrt {{{15}^2} + {{\left( {20} \right)}^2}} }} = 160{\rm{W}}\)