Biết cường độ dòng điện qua đoạn mạch chỉ có điện trở có biểu thức i=I0cos(ωt)A. Biểu thức điện áp đặt vào hai đầu đoạn mạch là:
Ta có:
+ uR luôn luôn cùng pha với i
+ Hiệu điện thế cực đại: U0=I0R
=> Biểu thức điện áp đặt vào hai đầu đoạn mạch: u=I0Rcos(ωt)V
Biết cường độ dòng điện qua đoạn mạch chỉ có cuộn cảm thuần có biểu thức i=I0cos(ωt)A. Biểu thức điện áp đặt vào hai đầu đoạn mạch là:
Ta có:
+ uL nhanh pha hơn i một góc π2
+ Điện áp cực đại: U0=I0ZL=I0.ωL
=> Biểu thức cường độ dòng điện qua cuộn cảm thuần là: u=I0ωLcos(ωt+π2)V
Biết cường độ dòng điện qua đoạn mạch chỉ có tụ điện có biểu thức i=I0cos(ωt)A. Biểu thức điện áp đặt vào hai đầu đoạn mạch là:
Ta có:
+ uC trễ pha hơn i một góc π2
+ Điện áp cực đại: U0=I0ZC=I0ωC
=> Biểu thức cường độ dòng điện qua cuộn cảm thuần là: u=I0ωCcos(ωt−π2)V
Đặt điện áp u=200√2cos100πt(V) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần 100 Ω và cuộn cảm thuần có độ tự cảm 1πH. Biểu thức cường độ dòng điện trong đoạn mạch là:
Áp dụng công thức tính tổng trở của mạch:
Z=√R2+(ωL)2=√1002+(100π.1π)2=100√2Ω
Cường độ dòng điện trong mạch là:
I=UZ=200100√2=√2A
Độ lệch pha giữa u và i được xác đinh bởi:
tanφ=ZLR=(100π.1π)100=1⇒φ=φu−φi=π4⇒φi=−π4
Phương trình cường độ dòng điện là:
i=2.cos(100πt−π4)A
Đồ thị cường độ dòng điện như hình vẽ
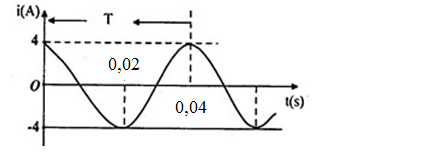
Cường độ dòng điện tức thời có biểu thức
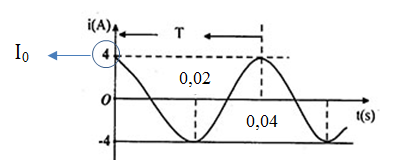
Từ đồ thị ta có:
+ Chu kì: T=0,04s→ω=2πT=2π0,04=50π(rad/s)
+ Cường độ dòng điện cực đại: I0=4(A)
+ Tại t = 0: i=4↔I0cosφ=4→cosφ=1→φ=0
=> Biểu thức cường độ dòng điện tức thời: i=4cos(50πt)A
Biểu thức cường độ dòng điện qua mạch chỉ có điện trở Rcó dạng i=2√2cos(100πt+π2)A. Biết điện trở có giá trị R=10Ω, biểu thức điện áp của mạch là:
+ Ta có u=iR=2√2.10cos(100πt+π2)=20√2cos(100πt+π2)V
Đặt vào hai đầu cuộn thuần cảm L=1πH một hiệu điện thế: u=200cos(100πt+π3)V . Biểu thức của cường độ dòng điện trong mạch là:
Ta có:
+ Cảm kháng: ZL=ωL=100π.1π=100Ω
+ uL sớm pha hơn i một góc π2, ta suy ra: φu−φi=π2→φi=φu−π2=π3−π2=−π6
+ Cường độ dòng điện cực đại: I0=U0ZL=200100=2A
=> Biểu thức cường độ dòng điện trong mạch: i=2cos(100πt−π6)A
Cho dòng điện i=4√2cos(100πt)A qua một ống dây thuần cảm có hệ số tự cảm L=120πH thì hiệu điện thế giữa hai đầu ống dây có dạng:
Ta có:
+ Cảm kháng: ZL=ωL=100π.120π=5Ω
+ uL sớm pha hơn i một góc π2, ta suy ra: φu−φi=π2→φu=φi+π2=0+π2=π2(rad)
+ Hiệu điện thế cực đại trong mạch: U0=I0.ZL=4√2.5=20√2V
=> Biểu thức điện áp trong mạch: u=20√2cos(100πt+π2)V
Đồ thị biểu diễn cường độ tức thời của dòng điện xoay chiều chỉ có cuộn cảm thuần có cảm kháng ZL=25Ω như hình sau:
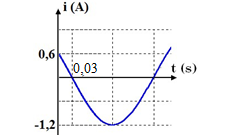
Viết biểu thức điện áp tức thời giữa hai đầu cuộn cảm?
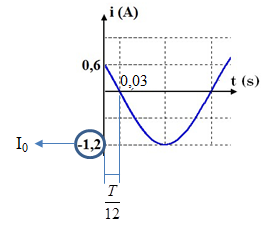
Từ đồ thị ta có:
+ T12=0,03s→T=0,36s→ω=2πT=2π0,36=50π9(rad/s)
+ Cường độ dòng điện cực đại: I0=1,2(A)
+ Tại t = 0: i = 0,6A và đang giảm: i=0,6↔I0cosφ=0,6→cosφ=0,61,2=12→φ=π3
=> Biểu thức cường độ dòng điện tức thời: i=1,2cos(50π9t+π3)A
+ Ta có uL nhanh pha hơn i một góc π2
+ Hiệu điện thế cực đại: U0=I0.ZL=1,2.25=30(V)
=> Biểu thức điện áp tức thời giữa hai đầu cuộn cảm:
u=30cos(50π9t+π3+π2)=30cos(50π9t+5π6)V
Mạch điện gồm cuộn dây thuần cảm, độ tự cảm L=14πH được gắn vào mạng điện xoay chiều người ta thấy dòng điện trong mạch có biểu thức là i=2cos(100πt−π6)A . Hỏi nếu gắn vào mạng điện đó đoạn mạch chỉ có điện trở R=50Ω thì dòng điện trong mạch có biểu thức là?
Theo đầu bài, ta có hiệu điện thế hai đầu đoạn mạch không thay đổi
+ Khi mạch chỉ có L thì cường độ dòng điện cực đại trong mạch là: I01=2A
+ Khi mạch chỉ có R thì cường độ dòng điện cực đại trong mạch là: I02
Mặt khác, ta có: {I01=U0ZLI02=U0R
Từ đó ta suy ra: I01I02=RZL
Lại có: \left\{ \begin{array}{l}{Z_L} = \omega L = 25\Omega \\R = 50\Omega \end{array} \right.
Từ đấy ta suy ra: \dfrac{{{I_{01}}}}{{{I_{02}}}} = \dfrac{R}{{{Z_L}}} = \dfrac{{50}}{{25}} = 2 \to {I_{02}} = \dfrac{{{I_{01}}}}{2} = \dfrac{2}{2} = 1A
Khi mạch có L, u sớm pha hơn i góc \dfrac{\pi }{2} \to {\varphi _u} = {\varphi _{{i_1}}} + \dfrac{\pi }{2}
Khi mạch có R, u cùng pha với i góc \to {\varphi _{{i_2}}} = {\varphi _u} = {\varphi _{{i_1}}} + \dfrac{\pi }{2} = - \dfrac{\pi }{6} + \dfrac{\pi }{2} = \dfrac{\pi }{3}
=> Biểu thức cường độ dòng điện trong mạch khi chỉ có R: {i_2} = cos\left( {100\pi t + \dfrac{\pi }{3}} \right)A
Mạch điện xoay chiều chỉ chứa cuộn cảm thuần L = \dfrac{1}{{3\pi }}H , hiệu điện thế xoay chiều ổn định đặt vào hai đầu mạch là u = {U_0}cos\left( {\omega t{\rm{ }} + \dfrac{\pi }{4}} \right){\rm{ }}V . Tại thời điểm {t_1} ta có {u_1} = 20\sqrt 2 {\rm{ }}V và {i_1} = \dfrac{{\sqrt 2 }}{2}A , tại thời điểm {t_2} ta có {u_2} = - 20\sqrt 3 {\rm{ }}V và và {i_2} = - 0,5A . Hãy hoàn thiện biểu thức của điện áp u.
Do mạch chỉ có L nên: u \bot i \to \dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1
Thay các giá trị, ta có:
\begin{array}{l}\left\{ \begin{array}{l}\dfrac{{{{(20\sqrt 2 )}^2}}}{{U_0^2}} + \dfrac{{{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2}}}{{I_0^2}} = 1{\rm{ (1)}}\\\dfrac{{{{\left( {20\sqrt 3 } \right)}^2}}}{{U_0^2}} + \dfrac{{{{\left( {0,5} \right)}^2}}}{{I_0^2}} = 1{\rm{ (2)}}\end{array} \right.\\ \to \dfrac{{400}}{{U_0^2}} = \dfrac{{0,25}}{{I_0^2}} \to \dfrac{{{U_0}}}{{{I_0}}} = 40 = {Z_L}\end{array}
Lại có,
\begin{array}{l}{Z_L} = \omega L\\ \to \omega = \dfrac{{{Z_L}}}{L} = \dfrac{{40}}{{\dfrac{1}{{3\pi }}}} = 120\pi \left( {rad/s} \right)\end{array}
Thay {I_0} = \dfrac{{{U_0}}}{{40}} vào (1) , ta được: \dfrac{{{{(20\sqrt 2 )}^2}}}{{U_0^2}} + \dfrac{{{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^2}}}{{\dfrac{{U_0^2}}{{{{40}^2}}}}} = 1 \to {U_0} = 40(V)
\to u = 40cos\left( {120\pi t + \dfrac{\pi }{4}} \right){\rm{ }}V
Đặt điện áp u{\rm{ }} = {U_0}cos(100{\rm{ }}\pi t + \dfrac{\pi }{3}){\rm{ }}V vào hai đầu một cuộn cảm thuần có hệ số tự cảm L = \dfrac{1}{{2\pi }}H. Ở thời điểm điện áp giữa hai đầu cuộn cảm là 150V thì cường độ dòng điện trong mạch là 4A. Biểu thức của cường độ dòng điện trong mạch là:
+ Cảm kháng: {Z_L} = \omega L = 100\pi .\dfrac{1}{{2\pi }} = 50\Omega
+ Do mạch chỉ có L nên: u \bot i \to \dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1
Lại có: {U_0} = {I_0}{Z_L}
\to \dfrac{{{{150}^2}}}{{{{(50.{I_0})}^2}}} + \dfrac{{{4^2}}}{{I_0^2}} = 1 \to {I_0} = 5(A)
Ta có {u_L} nhanh pha hơn i một góc \dfrac{\pi }{2}
\to {\varphi _u} - {\varphi _i} = \dfrac{\pi }{2} \to {\varphi _i} = {\varphi _u} - \dfrac{\pi }{2} = \dfrac{\pi }{3} - \dfrac{\pi }{2} = - \dfrac{\pi }{6}\left( {rad} \right)
\to i = 5cos(100\pi t - \dfrac{\pi }{6}){\rm{ }}A
Đặt điện áp xoay chiều u = 200\sqrt 2 .\cos \left( {100\pi t} \right)\,\,\left( V \right) vào hai đầu đoạn mạch gồm tụ điện có dụng kháng {Z_C} = 50\Omega mắc nối tiếp với điện trở thuần R = 50\Omega . Cường độ dòng điện trong mạch có biểu thức:
Cường độ dòng điện cực đại chạy trong mạch:
{I_0} = \dfrac{{{U_0}}}{{\sqrt {{R^2} + Z_C^2} }} = \dfrac{{200\sqrt 2 }}{{\sqrt {{{50}^2} + {{50}^2}} }} = 4A
Độ lệch pha giữa u và i:
\begin{array}{l}\tan \varphi = - \dfrac{{{Z_C}}}{R} = - \dfrac{{50}}{{50}} = - 1\\ \Rightarrow \varphi = {\varphi _u} - {\varphi _i} = - \dfrac{\pi }{4} \Rightarrow {\varphi _i} = {\varphi _u} + \dfrac{\pi }{4} = \dfrac{\pi }{4}\end{array}
Biểu thức của cường độ dòng điện: i = 4.\cos \left( {100\pi t + \dfrac{\pi }{4}} \right)A
Đặt điện áp xoay chiều u{\rm{ }} = {U_0}cos(100{\rm{ }}\pi t + \dfrac{{5\pi }}{6}){\rm{ }}V vào hai đầu một cuộn cảm thuần có độ tự cảm \dfrac{1}{{4\pi }}{\rm{ }}H . Ở thời điểm điện áp giữa hai đầu cuộn cảm là 100\sqrt 2 {\rm{ }}V thì cường độ dòng điện qua cuộn cảm là 2A. Biểu thức của cường độ dòng điện qua cuộn cảm là:
+ Cảm kháng: {Z_L} = \omega L = 100\pi .\dfrac{1}{{4\pi }} = 25\Omega
+ Do mạch chỉ có cuộn dây nên: u \bot i \to \dfrac{{{u^2}}}{{U_0^2}} + \dfrac{{{i^2}}}{{I_0^2}} = 1
Ta có: {Z_L} = 25\Omega \to {U_0} = 25{I_0}
\to \dfrac{{{{(100\sqrt 2 )}^2}}}{{{{(25{I_0})}^2}}} + \dfrac{{{2^2}}}{{I_0^2}} = 1 \to {I_0} = 6(A)
Mạch có cuộn dây nên {u_L} nhanh pha hơn i một góc \dfrac{\pi }{2}
\begin{array}{l}{\varphi _u} - {\varphi _i} = \dfrac{\pi }{2}\\ \to {\varphi _i} = {\varphi _u} - \dfrac{\pi }{2} = \dfrac{{5\pi }}{6} - \dfrac{\pi }{2} = \dfrac{\pi }{3}\left( {rad} \right)\end{array}
\to i = 6{\rm{cos}}\left( {100\pi t + \dfrac{\pi }{3}} \right)A
Một đoạn mạch điện xoay chiều gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cảm kháng gấp đôi dung kháng. Dùng vôn kế xoay chiều (điện trở rất lớn) đo điện áp giữa hai đầu tụ điện và điện áp giữa hai đầu điện trở thì số chỉ của vôn kế là như nhau. Độ lệch pha của điện áp giữa hai đầu đoạn mạch so với cường độ dòng điện trong đoạn mạch là:
Ta có:
+ Cảm kháng gấp đôi dung kháng => {U_L} = {\rm{ }}2{U_C}
+ Dùng vôn kế xoay chiều (điện trở rất lớn) đo điện áp giữa hai đầu tụ điện và điện áp giữa hai đầu điện trở thì số chỉ của vôn kế là như nhau => {U_R} = {\rm{ }}{U_C}
Độ lệch pha giữa hai đầu đoạn mạch so với cường độ dòng điện trong đoạn mạch là:
\tan \varphi = \dfrac{{{U_L} - {U_C}}}{{{U_R}}} = \dfrac{{2{U_C} - {U_C}}}{{{U_C}}} = 1 \Rightarrow \varphi = \dfrac{\pi }{4}
Một mạch điện gồm R = 60\Omega , cuộn cảm thuần có độ tự cảm L = \dfrac{{0,4}}{\pi }H và tụ điện có điện dung C = \dfrac{{{{10}^{ - 4}}}}{\pi }F mắc nối tiếp, biết biểu thức cường độ dòng điện trong mạch là i = \sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{8}} \right)V. Biểu thức điện áp đặt vào hai đầu mạch điện là?
+ Ta có:
- Cảm kháng: {Z_L} = \omega L = 100\pi .\dfrac{{0,4}}{\pi } = 40\Omega
- Dung kháng: {Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi .\dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega
+ Tổng trở của mạch: Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} = \sqrt {{{60}^2} + {{\left( {40 - 100} \right)}^2}} = 60\sqrt 2 \Omega
+ Hiệu điện thế cực đại đặt vào mạch: {U_0} = {I_0}Z = \sqrt 2 .60\sqrt 2 = 120V
+ Độ lệch pha của u so với i là: \tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = \dfrac{{40 - 100}}{{60}} = - 1 \to \varphi = - \dfrac{\pi }{4}
=> u chậm pha hơn i một góc - \dfrac{\pi }{4}
=> {\varphi _u} = {\varphi _i} - \dfrac{\pi }{4} = \dfrac{\pi }{8} - \dfrac{\pi }{4} = - \dfrac{\pi }{8}\left( {rad} \right)
=> Biểu thức điện áp đặt vào mạch: u = 120cos\left( {100\pi t - \dfrac{\pi }{8}} \right)V
Đặt điện áp u{\rm{ }} = 120\sqrt 2 cos100\pi t{\rm{ }}\left( V \right) vào hai đầu đoạn mạch nối tiếp gồm điện trở 150\Omega , tụ điện có điện dung \dfrac{{200}}{\pi }\mu Fvà cuộn cảm thuần có độ tự cảm \dfrac{2}{\pi }H. Biểu thức cường độ dòng điện trong đoạn mạch là:
- Ta có:
+ Cảm kháng của đoạn mạch: {Z_L} = \omega L = 200\Omega
+ Dung kháng của đoạn mạch: {Z_C} = \dfrac{1}{{\omega C}} = 50\Omega
- Tổng trở: Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} = 150\sqrt 2 \Omega
- Cường độ dòng điện cực đại: {I_0} = \dfrac{{{U_0}}}{Z} = 0,8A
- Độ lệch pha giữa u và i:
\begin{array}{l}\tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R} = 1 \Rightarrow \varphi = \dfrac{\pi }{4} \Rightarrow {\varphi _i} = - \dfrac{\pi }{4}\\ \Rightarrow i = 0,8\cos \left( {100\pi t - \dfrac{\pi }{4}} \right)A\end{array}
Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cảm kháng của cuộn cảm bằng 3 lần dung kháng của tụ điện. Tại thời điểm t, điện áp tức thời giữa hai đầu điện trở và điện áp tức thời giữa hai đầu tụ điện có giá trị tương ứng là 60 V và 20 V. Khi đó điện áp tức thời giữa hai đầu đoạn mạch là:
Ta có: {Z_L} = 3{Z_C} \Rightarrow \left| {{u_L}} \right| = 3\left| {{u_C}} \right|
Tại thời điểm t: \left\{ \begin{array}{l}{u_R} = 60V\\{u_C} = 20V \Rightarrow {u_L} = - 60V\end{array} \right. \Rightarrow u = {u_R} + {u_L} + {u_C} = 60 - 60 + 20 = 20V
Đặt điện áp u{\rm{ }} = {\rm{ }}{U_0}cos100\pi t{\rm{ }}\left( V \right) vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần 100\sqrt 3 \Omega mắc nối tiếp với cuộn cảm thuần có độ tự cảm L. Đoạn mạch MB chỉ có tụ điện có điện dung \dfrac{{{{10}^{ - 4}}}}{{2\pi }}F. Biết điện áp giữa hai đầu đoạn mạch AM lệch pha \dfrac{\pi }{3} so với điện áp giữa hai đầu đoạn mạch AB. Giá trị của L bằng
Dung kháng: {Z_C} = \dfrac{1}{{\omega C}} = 200\Omega
Ta có: \tan \varphi = \dfrac{{{Z_L} - {Z_C}}}{R};\tan {\varphi _{AM}} = \dfrac{{{Z_L}}}{R}
Có:
\begin{array}{l}\varphi - {\varphi _{AM}} = - \dfrac{\pi }{3} \Rightarrow \tan \left( {\varphi - {\varphi _{AM}}} \right) = \dfrac{{\tan \varphi - \tan {\varphi _{AM}}}}{{1 + \tan \varphi .\tan {\varphi _{AM}}}} = - \sqrt 3 \\ \Rightarrow \dfrac{{\dfrac{{{Z_L} - {Z_C}}}{R} - \dfrac{{{Z_L}}}{R}}}{{1 + \dfrac{{{Z_L} - {Z_C}}}{R}.\dfrac{{{Z_L}}}{R}}} = \dfrac{{ - R{Z_C}}}{{{R^2} + Z_L^2 - {Z_C}{Z_L}}} = - \sqrt 3 \\ \Rightarrow Z_L^2 - {Z_C}{Z_L} + {R^2} - \dfrac{{R{Z_C}}}{{\sqrt 3 }} = 0 \Rightarrow Z_L^2 - 200{Z_L} + 10000 = 0\\ \Rightarrow {Z_L} = 100\Omega \Rightarrow L = \dfrac{{{Z_L}}}{\omega } = \dfrac{1}{\pi }H\end{array}
Một đoạn mạch xoay chiều nối tiếp có điện trở R = 50\,\,\Omega , cuộn dây thuần cảm có độ tự cảm L = \dfrac{1}{{2\pi }}\,\,H. Đặt vào hai đầu đoạn mạch điện áp xoay chiều u = 220\sqrt 2 \cos 100\pi t\,\,V. Biểu thức cường độ dòng điện tức thời chạy trong mạch là
Cảm kháng của cuộn dây là: {Z_L} = \omega L = 100\pi .\dfrac{1}{{2\pi }} = 50\,\,\left( \Omega \right)
Tổng trở của mạch là: Z = \sqrt {{R^2} + {Z_L}^2} = \sqrt {{{50}^2} + {{50}^2}} = 50\sqrt 2 \,\,\left( \Omega \right)
Cường độ dòng điện cực đại trong mạch là: {I_0} = \dfrac{{{U_0}}}{Z} = \dfrac{{220\sqrt 2 }}{{50\sqrt 2 }} = 4,4\,\,\left( A \right)
Độ lệch pha giữa điện áp hai đầu đoạn mạch và cường độ dòng điện là:
\tan \varphi = \dfrac{{{Z_L}}}{R} = \dfrac{{50}}{{50}} = 1 \Rightarrow \varphi = {\varphi _u} - {\varphi _i} = \dfrac{\pi }{4} \Rightarrow 0 - {\varphi _i} = \dfrac{\pi }{4} \Rightarrow {\varphi _i} = - \dfrac{\pi }{4}\,\,\left( {rad} \right)
Vậy phương trình cường độ dòng điện trong mạch là: i = 4,4\cos \left( {100\pi t - \dfrac{\pi }{4}} \right)\,\,\left( A \right)

