Đặt nguồn âm điểm phát đẳng hướng trong môi trường truyền âm đồng tính không hấp thụ âm. Di chuyển một thiết bị đo mức cường độ âm dọc theo một đường thẳng trong môi trường đó thì thấy mức cường độ âm tại vị trí ban đầu có giá trị \(40 dB\), tăng dần đến giá trị cực đại bằng \(60 dB\) rồi giảm dần và có mức cường độ âm là \(50 dB\) tại vị trí dừng lại. Biết quãng đường di chuyển của thiết bị đo là \(60 m\). Khoảng cách ngắn nhất giữa thiết bị đo với nguồn phát âm gần nhất với giá trị nào sau đây
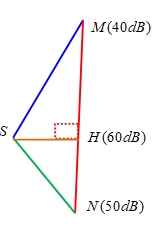
\(\left\{ \begin{array}{l}\underbrace {{L_H} - {L_M}}_{20(dB)} = 20\log \dfrac{{SM}}{{SH}} \to SM = 10SH\\\underbrace {{L_H} - {L_N}}_{10(dB)} = 20\log \dfrac{{SN}}{{SH}} \to SN = \sqrt {10} SH\end{array} \right. \to MH + HN = \underbrace {\sqrt {S{M^2} - S{H^2}} }_{SH\sqrt {99} } + \underbrace {\sqrt {S{N^2} - S{H^2}} }_{SH.3} = 60\)
=> \(SH \approx \)\(4,633(m)\)
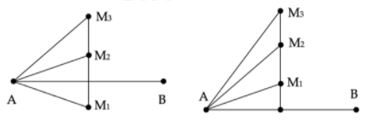
Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn đặt tại hai điểm \(A,B\) ở mặt nước dao động điều hòa cùng tần số, cùng pha. Hai điểm cực tiểu liên tiếp trên đoạn \(AB\) cách nhau \(2\;{\rm{cm}}\). Khoảng cách giữa hai nguồn là \(AB = 30\;{\rm{cm}}\). Xét các phần tử nước nằm trên trung trực của \(AB,\,\,{M_1},\,\,{M_2},\,\,{M_3}\) theo thứ tự đó là ba điểm liên tiếp mà phần tử mặt nước ở đó dao động cùng pha với nguồn. Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) gần nhất với giá trị nào sau đây?
Hai điểm cực tiểu liên tiếp trên đoạn \(AB\) cách nhau \(2\;{\rm{cm}}\)\( \Rightarrow \frac{\lambda }{2} = 2 \Rightarrow \lambda = 4cm.\)
Trên trung trực của \(AB\) có 3 điểm liên liếp \({M_1},\,\,{M_2},\,\,{M_3}\) dao động cùng pha với nguồn và cách nhau xa nhất như hình vẽ.
Để \(M\) cùng pha nguồn thì:
\(AM = k\lambda \ge \frac{{AB}}{2} \Leftrightarrow k.4 \ge 15 \Rightarrow k \ge 3,74 \Rightarrow {k_{\min = 4}}\)
TH1: \({M_1},\,\,{M_2}\) cùng phía với \(AB\) thì lần lượt có \(k = 4,\,5,\,\,6\)
Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) khi này là:
\(\begin{array}{l}{M_1}{M_3} = \sqrt {AM_3^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} - \sqrt {AM_1^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} \\ \Rightarrow {M_1}{M_3} = \sqrt {{{24}^2} - {{15}^2}} - \sqrt {{{16}^2} - {{15}^2}} \approx 13,2\left( {cm} \right)\end{array}\)
TH2: \({M_1},\,\,{M_2}\)khác phía với \(AB\) thì \({M_1}\)và \({M_2}\) đều có \(k = 4\) và \({M_3}\) có \(k = 5.\)
Khoảng cách lớn nhất giữa \({M_1}\) và \({M_3}\) khi này là:
\(\begin{array}{l}{M_1}{M_3} = \sqrt {AM_1^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} + \sqrt {AM_3^2 - {{\left( {\frac{{AB}}{2}} \right)}^2}} \\ \Rightarrow {M_1}{M_3} = \sqrt {{{16}^2} - {{15}^2}} + \sqrt {{{24}^2} - {{15}^2}} \approx 18,8\left( {cm} \right)\end{array}\)
Cho ống sáo có 1 đầu bịt kín và 1 đầu để hở. Biết rằng ống sáo phát ra âm to nhất ứng với hai giá trị tần số của hai họa âm liên tiếp là \(150Hz\) và \(250Hz\). Tần số âm nhỏ nhất khi ống sáo phát ra âm to nhất bằng:
Ống sáo một đầu kín, một đầu hở: \(\ell = \left( {2k + 1} \right)\frac{\lambda }{4} = (2k + 1)\frac{v}{{4f}} \Rightarrow f = \frac{{(2k + 1)v}}{{4\ell }}\)
Theo bài ra ta có: \(\left\{ \begin{array}{l}150 = \frac{{(2k + 1)v}}{{4\ell }}\\250 = \frac{{(2(k + 1) + 1)v}}{{4\ell }} = \frac{{(2k + 3)v}}{{4\ell }}\end{array} \right.\)
Từ đó tìm được \(\frac{v}{\ell } = 200\)
Tần số âm nhỏ nhất ứng với \({k_{min}} = {\rm{ }}0\). Thay vào ta được \(f = \frac{v}{{4l}} = \frac{{200}}{4} = 50{\rm{ }}Hz\)
Tại vị trí $O$ trên mặt đất có một nguồn âm điểm phát âm đẳng hướng ra không gian với công suất không đổi. Hai điểm $P$ và $Q$ lần lượt trên mặt đất sao cho $OP$ vuông góc với $OQ$. Một thiết bị xác định mức cường độ âm $M$ bắt đầu chuyển động thẳng với gia tốc $a$ không đổi từ $P$ hướng đến $Q$, sau khoảng thời gian $t_1$ thì $M$ đo được mức cường độ âm lớn nhất; tiếp đó $M$ chuyển động thẳng đều và sau khoảng thời gian \(0,125{t_1}\) thì đến điểm $Q$. Mức cường độ âm đo được tại $P$ là \(20{\rm{ }}dB\). Mức cường độ âm tại $Q$ mà máy đo được là:
+ Ta có hình vẽ sau
+ Sau khoảng thời gian \({t_1}\) thì $M$ đo được mức cường độ âm lớn nhất => máy đi được quãng đường \(PH = \dfrac{{at_1^2}}{2}\), và vận tốc của máy tại H là \(v = a{t_1}\)
+ Sau đó vật chuyển động thẳng đều và đi được quãng đường HQ trong thời gian \(0,125{t_1}\)
=>\(HQ = v.t =a{t_1}.0,125{t_1} = 0,125at_1^2\)
=> Cạnh huyền \(PQ = PH + HQ = 0,625at_1^2\)
+ Theo hệ thức lượng trong tam giác vuông ta có
\(OP = \sqrt {PH.PQ} = \sqrt {0,5.0,625} at_1^2\) ; \(OQ = \sqrt {HQ.PQ} = \sqrt {0,125.0,625} at_1^2\)
Ta có \({L_Q} - {L_P} = 10log\dfrac{{O{P^2}}}{{O{Q^2}}} = 10log\dfrac{{0,5.0,625}}{{0,125.0,625}} = 6\)
\( \to {L_Q}{\rm{ = }}{L_P} + 6 = 26dB\)
Một sợi dây đàn hồi có chiều dài \(l = 60cm\) và hai đầu dây cố định. Khi được kích thích dao động, trên dây hình thành sóng dừng với \(4\) bó sóng và biên độ dao động tại bụng là \(4cm\). Tại M gần nguồn phát sóng tới (tại A) nhất có biên độ dao động là \(2\sqrt 3 cm\). Đoạn MA dài:
Sử dụng điều kiện để có sóng dừng với trường hợp 2 đầu dây cố định \(l = k\frac{\lambda }{2}\) , trong đó k là só bó sóng. Mà óng dừng trong trường hợp trên có 4 bó sóng nên \(k{\rm{ }} = {\rm{ }}4\) nên ta có \(l = k\dfrac{\lambda }{2} \Leftrightarrow 60 = 4.\dfrac{\lambda }{2} \Leftrightarrow \lambda = 30cm\)
Bụng sóng dao động với biên độ là: \(2a{\text{ }} = {\text{ }}4cm \to a{\text{ }} = {\text{ }}2cm\)
Điểm M dao động với biên độ \(2\sqrt 3 = a\sqrt 3 \) nên M sẽ cách điểm nút gần nó nhất một khoảng là \(\dfrac{\lambda }{6} = \dfrac{{30}}{6} = 5cm\)
Trong hiện tượng giao thoa sóng nước hai nguồn kết hợp A, B cách nhau một khoảng \(a = 20cm\) dao động điều hòa theo phương thẳng đứng, cùng pha, cùng tần số \(50{\rm{ }}Hz\). Tốc độ truyền sóng trên mặt nước là \(1,5{\rm{ }}m/s\). Xét các điểm trên mặt nước thuộc đường tròn tâm A, bán kính AB, điểm nằm trên đường tròn dao động với biên độ cực đại cách đường trung trực của AB gần nhất một khoảng:
Để M là cực đại và gần trung trực của AB nhất thì M phải nằm trên hypebol ứng với \(k = 1\)
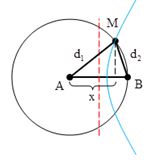
+ Ta có:
\({d_1} - {d_2} = \lambda {k} = 17cm\)
\(\begin{array}{l}\left\{ \begin{array}{l}{h^2} = {20^2} - {x^2}\\{h^2} = {17^2} - {\left( {20 - x} \right)^2}\end{array} \right.\\ \Rightarrow {20^2} - {x^2} = {17^2} - {\left( {20 - x} \right)^2}\\ \Rightarrow x = 12,775cm\end{array}\)
Vậy khoảng cách từ M đến trung trực sẽ là \(2,775{\rm{ }}cm\)
Trên một sợi dây đàn hồi đang có sóng dừng ổn định. Ba điểm \(M,{\rm{ }}N,{\rm{ }}P\) là ba điểm liên tiếp trên dây dao động với cùng biên độ \(4{\rm{ }}cm\), biết M, N dao động cùng pha, \(N,{\rm{ }}P\) dao động ngược pha. Khi các điểm qua vị trị cân bằng khoảng cách \(MN{\rm{ }} = {\rm{ }}2NP{\rm{ }} = {\rm{ }}20{\rm{ }}cm\). Biên độ của bụng sóng và bước sóng:
Theo đề bài ta vẽ được hình dạng sóng dừng như bên:
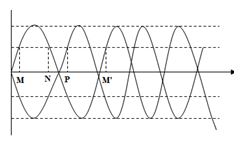
Từ \(M\) đến \(M'\) là một bước sóng.
Dựa vào hình vẽ tính được
\(\lambda = MM' = 2\left( {MN + NP} \right) = 60cm\)
\(P\) là điểm gần nút sóng nhất có biên độ \(4cm\), cách nút sóng một đoạn bằng \(\dfrac{{NP}}{2} = 5cm\) . Ta có:
\({A_P} = 2A\left| {\cos \left( {\dfrac{{2\pi .d}}{\lambda } + \dfrac{\pi }{2}} \right)} \right| = 2A\left| {\cos \left( {\dfrac{{2\pi .5}}{{60}} + \dfrac{\pi }{2}} \right)} \right| = 4cm \Rightarrow A = 4cm\)
Vậy biên độ bụng sóng là \(2A = 8cm\)
Tại mặt chất lỏng có hai nguồn phát sóng kết hợp \(A,{\rm{ }}B\) cách nhau \(16{\rm{ }}cm\), dao động điều hòa theo phương vuông góc mặt chất lỏng với phương trình: \({u_A} = 2\cos 40\pi t\left( {cm} \right)\) và \({u_B} = 2\cos \left( {40\pi t + \pi } \right)\left( {cm} \right)\). Tốc độ truyền sóng trên mặt chất lỏng là \(40{\rm{ }}cm/s\). \(M\) là một điểm trên đường thẳng \(Ax\) vuông góc với \(AB\) mà tại đó các phần tử chất lỏng dao động với biên độ cực đại. Khoảng cách \(AM\) ngắn nhất bằng:
\(\lambda = \dfrac{v}{f} = \dfrac{{40}}{{20}} = 2cm\)
- Cách 1:
+ Số điểm dao động với biên độ cực đại trên đoạn AB:
\(\dfrac{{ - AB}}{\lambda } - \dfrac{1}{2} < k < \dfrac{{AB}}{\lambda } - \dfrac{1}{2}\)
\( \Rightarrow - 8,5 < k < 7,5\)
\( \to \) Có \(16\) điểm dao động với biên độ cực đại.
+ Điểm M gần A nhất thì M nhất định nằm trên vân cực đại ứng với bậc \(k = - 7,5\) (Số bán nguyên nhỏ hơn \(8,5\)).
\(MA - \sqrt {A{B^2} + M{A^2}} = - 7,5\lambda \)
\(MA - \sqrt {{{16}^2} + M{A^2}} = - 7,5.2 \Rightarrow MA = 1,03cm\)
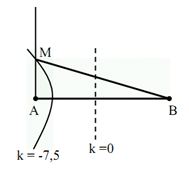
- Cách 2:
+ Số dao động cực đại trên đoạn AB: \( - \dfrac{1}{2} - \dfrac{{AB}}{\lambda } \le k \le \dfrac{{AB}}{\lambda } - \dfrac{1}{2} \Leftrightarrow - 8,5 \le k \le 7,5\)
+ Để \(AM\) ngắn nhất thì \(M\) phải nằm trên hypebol cực đại \(k = - 8\)
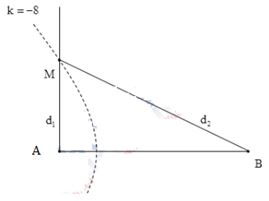
Từ hình vẽ ta có \(\left\{ \begin{array}{l}{d_2} - {d_1} = 15\\d_2^2 = 16 + d_1^2\end{array} \right. = > {\left( {{d_1} + 15} \right)^2} = {16^2} + d_1^2\)
Giải phương trình thu được \({d_1} = {\rm{ }}1,03{\rm{ }}cm\)
Trên bề mặt chất lỏng cho hai nguồn sóng \({O_1},{O_2}\) cách nhau \(24cm\) có phương trình lần lượt \({u_1} = {\rm{ }}{u_2} = 6cos(40\pi t - \dfrac{\pi }{2}){\rm{ }}\left( {mm} \right)\). Cho tốc độ truyền sóng trên bề mặt chất lỏng \(80\left( {cm/s} \right)\). Tại thời điểm t sóng từ nguồn \({O_1}\) vừa truyền tới trung điểm của đoạn thẳng \({O_1}{O_2}\). Xét phần tử phần tử \(M\)có vị trí cân bằng cách \({O_1},{\rm{ }}{O_2}\) lần lượt \(32\left( {cm} \right)\) và \(38\left( {cm} \right)\). Li độ của \(M\) sau thời điểm t một khoảng \(\dfrac{{31}}{{120}}s\) là:
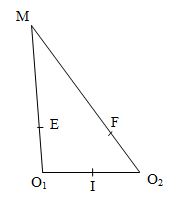
Ta có: ${u_1} = {u_2} = 6cos(40\pi t - \dfrac{\pi }{2}){\text{ }}\left( {mm} \right)$
+ Bước sóng $\lambda = \dfrac{v}{f} = \dfrac{{80}}{{20}} = 4(cm)$
+ Tại thời điểm t, sóng do nguồn ${O_1}$ vừa truyền tới trung điểm $I$ của đoạn ${O_1}{O_2}$
→ Sóng ở hai nguồn truyền đi được quãng đường $12{\rm{ }}cm = 3\lambda $ (hết thời gian $3T$)
Xét thời điểm sau thời điểm t một khoảng $\dfrac{{31}}{{120}}s = 5T + \dfrac{T}{6}$
Khi đó chỉ có sóng ở nguồn $1$ truyền đến $M$
Thật vậy, $EM{\rm{ }} = {\rm{ }}20cm{\rm{ }} = {\rm{ }}5\lambda $ → Cần thời gian $5T$ để sóng truyền từ $E$ đến $M$
→ sau $\dfrac{{31}}{{120}}s = 5T + \dfrac{T}{6}$ sóng nguồn $1$ truyền được đến $M$
$FM{\rm{ }} = {\rm{ }}26cm{\rm{ }} = {\rm{ }}6,5\lambda $ → Cần thời gian $6,5T$ để sóng truyền từ $F$ đến $M$
→ sau $\dfrac{{31}}{{120}}s = 5T + \dfrac{T}{6}$ sóng từ nguồn $2$ chưa đến $M$
Như vậy li độ của điểm M tại thời điểm sau thời điểm t một khoảng $\dfrac{{31}}{{120}}s = 5T + \dfrac{T}{6}$ là:
\(\begin{array}{l}{u_M} = {u_{1M}} = 6\cos (40\pi t - \dfrac{\pi }{2} - \dfrac{{2\pi {d_1}}}{\lambda })\\ = 6\cos \left[ {40\pi (3T + \dfrac{{31}}{{120}}) - \dfrac{\pi }{2} - \dfrac{{2\pi .32}}{4}} \right] = 3\sqrt 3 (cm)\end{array}\)
Cho \(4\) điểm \(O,{\rm{ }}M,{\rm{ }}N\) và \(P\) đồng phẳng, nằm trong một môi trường truyền âm. Trong đó, \(M\) và \(N\) nằm trên nửa đường thẳng xuất phát từ \(O\), tam giác \(MNP\) là tam giác đều. Tại \(O\), đặt một nguồn âm điểm có công suất không đổi, phát âm đẳng hướng ra môi trường. Coi môi trường không hấp thụ âm. Biết mức cường độ âm tại \(M\) và \(N\) lần lượt là \(50dB\) và \(40dB\). Mức cường độ âm tại \(P\) là:
Theo đề bài ta có hình vẽ sau:
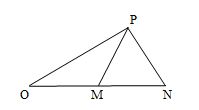
\({L_M} = {\text{ }}50dB,{\text{ }}{L_N} = {\text{ }}40dB\)
\(\begin{array}{l} \to {L_M} - {L_N} = 10\log \dfrac{{r_N^2}}{{r_M^2}} = 10\\ \to \dfrac{{r_N^2}}{{r_M^2}} = {10^1} \Rightarrow {r_N} = \sqrt {10} {r_M}\end{array}\)
Tam giác $MNP$ là tam giác đều cạnh $a$
=> \({r_N} = {\rm{ }}{r_M} + {\rm{ }}a\)
=> \({r_M} = \dfrac{a}{{\sqrt {10} - 1}};{r_N} = \dfrac{{a\sqrt {10} }}{{\sqrt {10} - 1}}\)
Áp dụng định lí hàm số sin trong tam giác $OPN$ ta có:
\(\begin{array}{l}O{P^2} = \sqrt {O{N^2} + P{N^2} - 2ON.PN.cos\widehat {ONP}} \\ \Leftrightarrow {r_P} = \sqrt {r_N^2 + {a^2} - 2.{r_N}.a.cos{{60}^0}} \\ = a\sqrt {{{\left( {\dfrac{{\sqrt {10} }}{{\sqrt {10} - 1}}} \right)}^2} + 1 - 2.\dfrac{{\sqrt {10} }}{{\sqrt {10} - 1}}.1.\dfrac{1}{2}} \approx 1,295a\end{array}\)
Khi đó
\(\begin{array}{l}{L_M} - {L_P} = 10\log \dfrac{{r_P^2}}{{r_M^2}} = 10\log \dfrac{{{{1,295}^2}}}{{{{\left( {\dfrac{1}{{\sqrt {10} - 1}}} \right)}^2}}} \approx 8,94\\ \Rightarrow {L_P} = {L_M} - 8,94 = 50 - 8,94 = 41,06dB \approx 41,1dB\end{array}\)
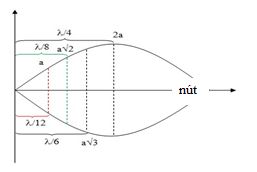
Trên sợi dây căng ngang, hai đầu cố định có sóng dừng với tần số dao động là \(5{\rm{ }}Hz\). Biên độ của điểm bụng là \(2{\rm{ }}cm\). Ta thấy khoảng cách giữa hai điểm trong một bó sóng có cùng biên độ \(1{\rm{ }}cm\) là \(10{\rm{ }}cm\). Tốc độ truyền sóng trên dây là:
+ Biên độ dao động tại điểm cách nút một đoạn $d$ được xác định bởi
\({a_M} = 2{\rm{a}}\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right|\) với $2a$ là biên độ của điểm bụng
\( \Rightarrow \) điểm dao động với biên độ $a$ sẽ cách nút một khoảng \(\dfrac{\lambda }{{12}}\)
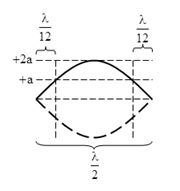
Ta có :
\(\dfrac{\lambda }{2} - \left( {\dfrac{\lambda }{{12}} + \dfrac{\lambda }{{12}}} \right) = 10 \Rightarrow \lambda = 30cm\)
Tốc độ truyền sóng trên dây : \(v = \lambda f = 30.5 = 150cm/s\)
Tại mặt chất lỏng có hai nguồn phát sóng \(A,{\rm{ }}B\) giống nhau và cách nhau một đoạn \(10{\rm{ }}cm\). Gọi \(M\)và \(N\) là hai điểm thuộc mặt chất lỏng sao cho \(MN{\rm{ }} = {\rm{ }}8{\rm{ }}cm\) và \(ABMN\) là hình thang cân (\(AB\) song song với \(MN\)). Bước sóng của sóng trên mặt chất lỏng do hai nguồn phát ra là \(1{\rm{ }}cm\). Để trong đoạn \(MN\) có \(7\) điểm dao động với biên độ cực đại thì diện tích lớn nhất của hình bình hành là:
Để diện tích $ABMN$ là lớn nhất thì $AH$ phải lớn nhất điều này xảy ra khi $N$ nằm tên cực đại thứ $3$
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}NB - NA = 3\lambda \\N{B^2} = N{H^2} + {9^2}\\N{A^2} = N{H^2} + 1\end{array} \right.\\ \Rightarrow \sqrt {N{H^2} + 9} - \sqrt {N{H^2} + 1} = 3cm\\ \Rightarrow NH = 11,8cm\end{array}\)
Diện tích $ABMN$ khi đó là: \(S = \dfrac{1}{2}\left( {AB + MN} \right)NH = \dfrac{1}{2}\left( {10 + 8} \right)11,8 = 106,2c{m^2}\)
Trên một sợi dây căng ngang đang có sóng dừng. Xét ba điểm \(A,{\rm{ }}B\) và \(C\) với \(B\) là trung điểm của đoạn \(AC\). Điểm \(A\) cách điểm nút \(C\) một đoạn gần nhất \(10{\rm{ }}cm\). Khoảng thời gian ngắn nhất để hai lần liên tiếp điểm \(A\) có li độ bằng biên độ dao động của điểm \(B\) là \(0,2{\rm{ }}s\). Tốc độ truyền sóng trên dây là:
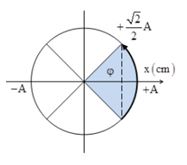
Biên độ dao động của phần tử khi có sóng dừng \(a = A\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right|\), với \(d\) là khoảng cách từ điểm đang xét đến nút gần nhất, \(A\) là biên độ bụng \({a_B} = A\left| {\sin \dfrac{{2\pi d}}{\lambda }} \right| = A\left| {\sin \dfrac{{2\pi \frac{\lambda }{8}}}{\lambda }} \right| = \dfrac{{\sqrt 2 }}{2}A\)
Ta thấy khoảng thời gian liên tiếp để li độ \(A\) bằng biên độ của \(B\) là:
\(\Delta t = 0,2s = \dfrac{T}{4} \Rightarrow T = 0,8s\)
Tốc độ truyền sóng trên dây \(v = \dfrac{\lambda }{T} = \dfrac{{4AC}}{T} = \dfrac{{4.10}}{{0,8}} = 50cm/s = 0,5m/s\)
Một vận động viên hằng ngày đạp xe trên đoạn đường thẳng từ điểm \(A\) đúng lúc còi báo thức bắt đầu kêu, khi đến điểm \(B\) thì còi vừa dứt. Mức cường độ âm tại \(A\) và \(B\) lần lượt là \(60{\rm{ }}dB\) và \(54{\rm{ }}dB\). Còi đặt tại \(O\), phát âm đẳng hướng với công suất không đổi và môi trường không hấp thụ âm; góc \(AOB\) bằng \({150^0}\) . Biết rằng vận động viên này khiếm thính nên chỉ nghe được mức cường độ âm từ \(66{\rm{ }}dB\) trở lên và tốc độ đạp xe không đổi, thời gian còi báo thức kêu là \(1\) phút. Trên đoạn đường \(AB\), vận động viên nghe thấy tiềng còi báo thức trong khoảng thời gian xấp xỉ bằng:
Tai của người người khiếm thính nghe được khi người đó đi từ M1 đến M2
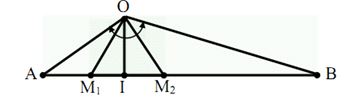
\(\left\{ \begin{gathered}
\underbrace {{L_A} - {L_B}}_{0,6} = \log \dfrac{{O{B^2}}}{{O{A^2}}} \hfill \\
\underbrace {{L_M} - {L_A}}_{0,6} = \log \dfrac{{O{A^2}}}{{OM_1^2}} \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
\dfrac{{O{B^2}}}{{O{A^2}}} = {10^{0,6}} \hfill \\
\dfrac{{O{A^2}}}{{OM_1^2}} = {10^{0,6}} \hfill \\
\end{gathered} \right.\xrightarrow{{OA = 1}}\left\{ \begin{gathered}
O{B^2} = {10^{0,6}} \hfill \\
O{M^2} = {10^{ - 0,6}} \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
OB = {10^{0,3}} \hfill \\
OM = {10^{ - 0,3}} \hfill \\
\end{gathered} \right.\)
\(\left\{ \begin{array}{l}AB = \sqrt {O{A^2} + O{B^2} - 2OA.OB\cos {{150}^0}} \approx 2,90\\{S_{\Delta OAB}} = \dfrac{1}{2}AB.OI = \dfrac{1}{2}OA.OB\sin {150^0} \Rightarrow OI \approx 0,34\end{array} \right.\)
\(0,5{M_1}{M_2} = \sqrt {OM_1^2 - O{I^2}} \approx 0,37 \Rightarrow {M_1}{M_2} \approx 0,74\)
\(\left\{ \begin{array}{l}AB = v.t\\{M_1}{M_2} = v.{t_1}\end{array} \right. \Rightarrow {t_1} = \dfrac{{{M_1}{M_2}}}{{AB}}.t = \dfrac{{0,74}}{{2,90}}.60 \approx 15s\)
Ở mặt nước có hai nguồn kết hợp đặt tại hai điểm \(A\) và \(B\), dao động cùng pha theo phương thẳng đứng, phát ra hai sóng có bước sóng \(\lambda \). Trên \(AB\) có \(9\) vị trí mà ở đó các phần tử nước dao động với biên độ cực đại. \(C\) và \(D\) là hai điểm ở mặt nước sao cho \(ABCD\) là hình vuông. \(M\) là một điểm thuộc cạnh \(CD\) và nằm trên vân cực đại giao thoa bậc nhất \(\left( {MA{\rm{ }} - {\rm{ }}MB{\rm{ }} = {\rm{ }}\lambda } \right)\). Biết phần tử tại \(M\) dao động cùng pha với các nguồn. Độ dài đoạn \(AB\) gần nhất với giá trị nào sau đây?
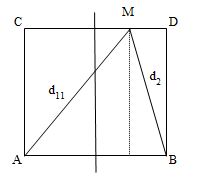
M là cực đại giao thoa và cùng pha với hai nguồn : \(\left\{ \begin{array}{l}{d_1} - {d_2} = n\lambda \\{d_1} + {d_2} = m\lambda \end{array} \right.(1)\) n và m là số nguyên cùng lẻ hoặc cùng chẵn.
Vì n = 1 => m là số lẻ. Trên hình, theo đề ta có :\(\left\{ \begin{array}{l}{d_1} + {d_2} > AB\\4\lambda \le AB < 5\lambda \end{array} \right.\left( 2 \right)\)
Từ (1) và (2) => \(\left\{ \begin{array}{l}{d_1} - {d_2} = \lambda \\{d_1} + {d_2} = 11\lambda \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{d_1} = 6\lambda \\{d_2} = 5\lambda \end{array} \right..\)
\(\sqrt {{6^2}{\lambda ^2} - A{B^2}} + \sqrt {{5^2}\lambda - A{B^2}} = AB \to AB = 4,8336\lambda \)
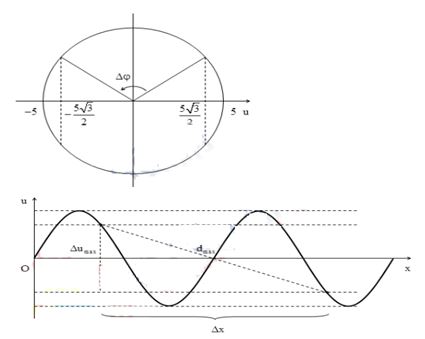
\(M\) và \(N\) là hai điểm trên một mặt nước phẳng lặng cách nhau một khoảng \(20cm\). Tại điểm \(O\) trên đường thẳng \(MN\) và nằm ngoài đoạn \(MN\), người ta đặt nguồn dao động theo phương vuông góc với mặt nước với phương trình \(u = 5\cos \omega t\left( {cm} \right)\), tạo ra sóng trên mặt nước với bước sóng \(\lambda = 15cm\). Khoảng cách xa nhất giữa hai phần tử môi trường tại \(M\) và \(N\) khi có sóng truyền qua là bao nhiêu?
Độ lệch pha giữa hai điểm M và N: \(\Delta \varphi = \dfrac{{2\pi x}}{\lambda } = \dfrac{{8\pi }}{3} = 2\pi + \dfrac{{2\pi }}{3}rad\)
Khoảng cách giữa M và N là lớn nhất khi hiệu li độ giữa chúng là lớn nhất ta có \(\Delta {u_{\max }} = 5\sqrt 3 cm\)
Vậy khoảng cách lớn giữa M và N là \(\)\({d_{\max }} = \sqrt {\Delta {x^2} + \Delta u_{\max }^2} \approx 21,79cm\)
Trong một trận đấu bóng đá, kích thước sân là dài \(105m\), rộng \(68m\). Trong một lần thổi phạt, thủ môn \(A\) của đội bị phạt đứng chính giữa hai cọc gôn, trọng tài đứng phía tay phải của thủ môn, cách thủ môn đó \(32,3m\) và cách góc sân gần nhất \(10,5m\). Trọng tài thổi còi và âm đi đẳng hướng thì thủ môn \(A\) nghe rõ âm thanh có mức cường độ âm \(40dB\). Khi đó huấn luyện viên trưởng của đội đang đứng phía trái thủ môn \(A\) và trên đường ngang giữa sân, phía ngoài sân, cách biên dọc \(5m\) sẽ nghe được âm thanh có mức cường độ âm có độ lớn xấp xỉ là:
Gọi $A,{\rm{ }}H,{\rm{ }}T$ lần lượt là vị trí thủ môn, huấn luyện viên và trọng tài.
Ta có hình sau:
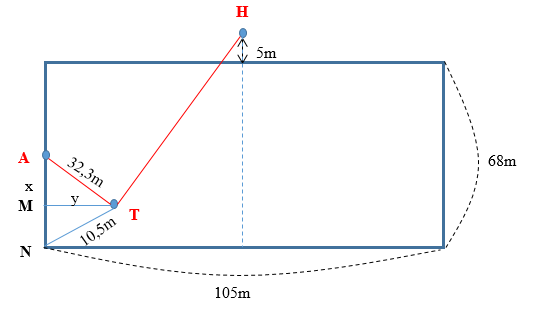
Tính x, y:
+ Xét \(\Delta ATM\) có :
\(\begin{array}{l}A{M^2} + M{T^2} = A{T^2}\\ \leftrightarrow {x^2} + {y^2} = 32,{3^2}{\rm{ }}\left( 1 \right)\end{array}\)
+ Xét \(\Delta MTN\) có :
\(\begin{array}{l}M{N^2} + M{T^2} = N{T^2} \leftrightarrow {\left( {AN - AM} \right)^2} + M{T^2} = N{T^2}\\ \leftrightarrow {\left( {\dfrac{{68}}{2} - x} \right)^2} + {y^2} = 10,{5^2}{\rm{ }}\left( 2 \right)\end{array}\)
Từ (1) và (2), ta suy ra :
\(\begin{array}{l}{y^2} = 32,{3^2} - {x^2} = 10,{5^2} - {\left( {34 - x} \right)^2}\\ \to 32,{3^2} - {x^2} = 10,{5^2} - \left( {{{34}^2} - 2.34x + {x^2}} \right)\\ \to x = 30,72m\\ \to y = 9,97m\end{array}\)
Từ hình, ta có :
\(\begin{array}{l}T{H^2} = {\left( {\dfrac{{105}}{2} - y} \right)^2} + {\left( {\dfrac{{68}}{2} + x + 5} \right)^2}\\ = {\left( {\dfrac{{105}}{2} - 9,97} \right)^2} + {\left( {\dfrac{{68}}{2} + 30,72 + 5} \right)^2}\\ \to TH = 81,69m\end{array}\)
Ta có, mức cường độ âm tại A : \({L_A} = 10\log \dfrac{{{I_A}}}{{{I_0}}} = 40dB\)
Mức cường độ âm tại H : \({L_H} = 10\log \dfrac{{{I_H}}}{{{I_0}}}\)
\(\begin{array}{l}{L_A} - {L_H} = 10\log \dfrac{{{I_A}}}{{{I_H}}} = 10\log \dfrac{{r_H^2}}{{r_A^2}}\\ = 10\log \dfrac{{T{H^2}}}{{A{H^2}}} = 10\log \dfrac{{81,{{69}^2}}}{{32,{3^2}}} \approx 8dB\\ \to {L_H} = {L_A} - 8 = 40 - 8 = 32dB\end{array}\)
Trên mặt nước có 2 nguồn sóng kết hợp dao động cùng pha tại \({S_1}\) và \({S_2}\). Biết sóng lan truyền trên mặt nước với bước sóng \(λ = 1 cm\) và \({S_1}{S_2}\)= \(5,4 cm\). Gọi \(Δ\) là đường trung trực thuộc mặt nước của \({S_1}{S_2}\), \(M, N, P, Q\) là 4 điểm không thuộc \(Δ\) dao động với biên độ cực đại, cùng pha với nguồn và gần \(Δ\) nhất. Trong 4 điểm \(M, N, P, Q\) khoảng cách giữa 2 điểm gần nhau nhất có giá trị gần nhất với giá trị nào sau đây?
+ M, N, P, Q thuộc hình chữ nhật , khoảng cách gần nhất bằng độ dài đoạn MN. Ta chỉ xét điểm M.
+ M dao động với biên độ cực đại: \({d_2} - {d_1} = k\lambda \)
+ M dao động cùng pha với nguồn: \(\left[ \begin{array}{l}\left\{ \begin{array}{l}{d_2} - {d_1} = {k_{le}}\lambda \\{d_2} + {d_1} = {n_{le}}\lambda > 5,4\lambda \end{array} \right.\\\left\{ \begin{array}{l}{d_2} - {d_1} = {k_{chan}}\lambda \\{d_2} + {d_1} = {n_{chan}}\lambda > 5,4\lambda \end{array} \right.\end{array} \right.\)
+ M gần Δ nhất thì \(\left[ \begin{array}{l}{d_2} - {d_1} = 1.\lambda ,{d_2} + {d_1} = 7\lambda \to \left\{ \begin{array}{l}{d_2} = 4\lambda \\{d_1} = 3\lambda \end{array} \right.\\{d_2} - {d_1} = 2.\lambda ,{d_2} + {d_1} = 6\lambda \to \left\{ \begin{array}{l}{d_2} = 4\lambda \\{d_1} = 2\lambda \end{array} \right.\end{array} \right.\)(loại)
+ \(λ = 1 cm\) => \(\sqrt {{3^2} - {{(MH)}^2}} + \sqrt {{4^2} - {{(MH)}^2}} = 5,4(cm) \\\to MH \approx 2,189(cm)\)
\( \to AH \approx 2,051;HO \approx 0,649 \\\to MN = 2HO \approx 1,298cm\)
Trong thí nghiệm giao thoa ánh sáng qua hệ hai khe I-âng, người ta gắn một máy đo cường độ sáng tại một vị trí cố định trên màn. Ban đầu, ta thu được vân sáng tại vị trí đặt máy đo. Di chuyển từ từ màn ảnh cùng với máy đo ra xa hai khe theo phương vuông góc với mặt phẳng chứa hai khe. Sự phụ thuộc của cường độ ánh sáng \(\left( I \right)\) do bởi máy đo theo khoảng cách \(L\) màn đã dịch chuyển so với vị trí ban đầu được biểu diễn như đồ thị trong hình vẽ. Khoảng cách giữa màn và hai khe I-âng lúc đầu gần nhất với giá trị nào sau đây?
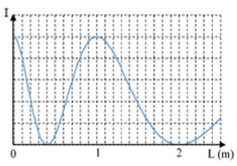
Từ đồ thị ta thấy:
Khi \(L = 0 \Rightarrow \) màn cách hai khe khoảng \({L_0}\), tại vị trí máy đo là vân sáng bậc \(k\)
Khi \(L = 1m \Rightarrow \)màn cách hai khe khoảng \({L_0} + 1\), tại vị trí máy đo là vân sáng bậc \(k + 1\)
Khi \(L = 2m \Rightarrow \) màn cách hai khe khoảng \({L_0} + 2\), tại vị trí máy đo là vân tối bậc \(k + 1,5\)
Tại vị trí máy đo có:
\(\begin{array}{l}x = \dfrac{{k\lambda {L_0}}}{a} = \dfrac{{\left( {k + 1} \right)\lambda \left( {{L_0} + 1} \right)}}{a} = \dfrac{{\left( {k + 1,5} \right)\lambda \left( {{L_0} + 2} \right)}}{a}\\ \Rightarrow \left\{ \begin{array}{l}k{L_0} = \left( {k + 1} \right)\left( {{L_0} + 1} \right)\\k{L_0} = \left( {k + 1,5} \right)\left( {{L_0} + 2} \right)\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}k = {L_0} + 1\\2k = 1,5{L_0} + 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}k = 3\\{L_0} = 2\,\,\left( m \right)\end{array} \right.\end{array}\)