Trong một trận đấu bóng đá, kích thước sân là dài \(105m\), rộng \(68m\). Trong một lần thổi phạt, thủ môn \(A\) của đội bị phạt đứng chính giữa hai cọc gôn, trọng tài đứng phía tay phải của thủ môn, cách thủ môn đó \(32,3m\) và cách góc sân gần nhất \(10,5m\). Trọng tài thổi còi và âm đi đẳng hướng thì thủ môn \(A\) nghe rõ âm thanh có mức cường độ âm \(40dB\). Khi đó huấn luyện viên trưởng của đội đang đứng phía trái thủ môn \(A\) và trên đường ngang giữa sân, phía ngoài sân, cách biên dọc \(5m\) sẽ nghe được âm thanh có mức cường độ âm có độ lớn xấp xỉ là:
Trả lời bởi giáo viên
Gọi $A,{\rm{ }}H,{\rm{ }}T$ lần lượt là vị trí thủ môn, huấn luyện viên và trọng tài.
Ta có hình sau:
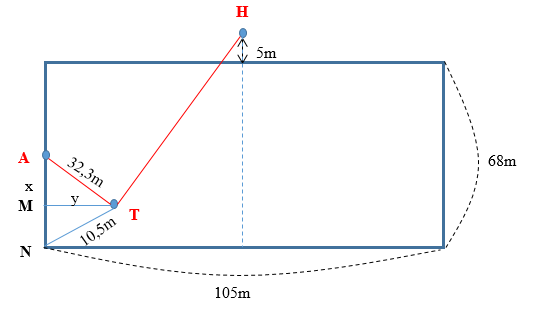
Tính x, y:
+ Xét \(\Delta ATM\) có :
\(\begin{array}{l}A{M^2} + M{T^2} = A{T^2}\\ \leftrightarrow {x^2} + {y^2} = 32,{3^2}{\rm{ }}\left( 1 \right)\end{array}\)
+ Xét \(\Delta MTN\) có :
\(\begin{array}{l}M{N^2} + M{T^2} = N{T^2} \leftrightarrow {\left( {AN - AM} \right)^2} + M{T^2} = N{T^2}\\ \leftrightarrow {\left( {\dfrac{{68}}{2} - x} \right)^2} + {y^2} = 10,{5^2}{\rm{ }}\left( 2 \right)\end{array}\)
Từ (1) và (2), ta suy ra :
\(\begin{array}{l}{y^2} = 32,{3^2} - {x^2} = 10,{5^2} - {\left( {34 - x} \right)^2}\\ \to 32,{3^2} - {x^2} = 10,{5^2} - \left( {{{34}^2} - 2.34x + {x^2}} \right)\\ \to x = 30,72m\\ \to y = 9,97m\end{array}\)
Từ hình, ta có :
\(\begin{array}{l}T{H^2} = {\left( {\dfrac{{105}}{2} - y} \right)^2} + {\left( {\dfrac{{68}}{2} + x + 5} \right)^2}\\ = {\left( {\dfrac{{105}}{2} - 9,97} \right)^2} + {\left( {\dfrac{{68}}{2} + 30,72 + 5} \right)^2}\\ \to TH = 81,69m\end{array}\)
Ta có, mức cường độ âm tại A : \({L_A} = 10\log \dfrac{{{I_A}}}{{{I_0}}} = 40dB\)
Mức cường độ âm tại H : \({L_H} = 10\log \dfrac{{{I_H}}}{{{I_0}}}\)
\(\begin{array}{l}{L_A} - {L_H} = 10\log \dfrac{{{I_A}}}{{{I_H}}} = 10\log \dfrac{{r_H^2}}{{r_A^2}}\\ = 10\log \dfrac{{T{H^2}}}{{A{H^2}}} = 10\log \dfrac{{81,{{69}^2}}}{{32,{3^2}}} \approx 8dB\\ \to {L_H} = {L_A} - 8 = 40 - 8 = 32dB\end{array}\)
Hướng dẫn giải:
+ Sử dụng biểu thức tính cường độ âm: $I = \dfrac{P}{S} = \dfrac{P}{{4\pi {r^2}}}$
+ Sử dụng biểu thức tính mức cường độ âm: \(L = 10\log \left( {\dfrac{I}{{{I_0}}}} \right)dB\)
+ Sử dụng biểu thức tính hiệu mức cường độ âm: \({L_A} - {L_B} = 10\log \left( {\dfrac{{{I_A}}}{{{I_B}}}} \right) = 10\log \left( {\dfrac{{r_B^2}}{{r_A^2}}} \right)\)

