Bài tập sóng cơ - Phương trình sóng cơ học

Trong khoảng thời gian $\Delta t = \left( {t + 2} \right) - t = 2s$, ta có:

+ Góc quét được $\Delta \varphi  = \omega \Delta t = \frac{\pi }{2}.2 = \pi$

+ Vẽ trên vòng tròn lượng giác, ta được:

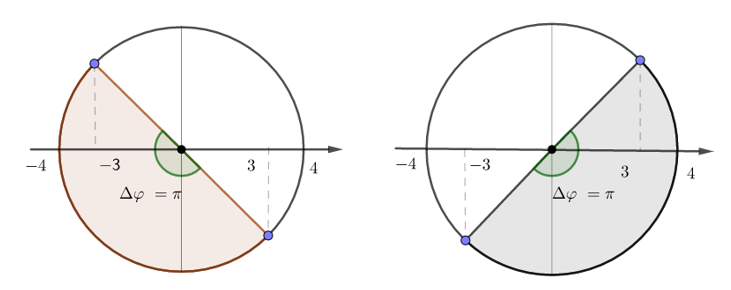
Từ vòng tròn lượng giác, ta có: $t{\rm{ }} + {\rm{ }}2s$ điểm M có li độ $3cm$

Ta có: $u = 6\cos \left( {4\pi t - 0,02\pi x} \right)$

Thay $x = \frac{{50}}{3}cm$ và $t = 2s$ vào, ta được: $u = 6\cos \left( {4\pi .2 - 0,02\pi .\frac{{50}}{3}} \right) = 6cos\left( {\frac{{23\pi }}{3}} \right) = 3cm$

Ta có: $\lambda  = \dfrac{v}{f} = \dfrac{{32}}{{\dfrac{{2\pi }}{{2\pi }}}} = 32cm$

Phương trình dao động tại M cách O một khoảng $x = 16cm$:

$\begin{array}{l}{u_M} = 4c{\rm{os}}\left( {2\pi t + \dfrac{\pi }{6} - \dfrac{{2\pi x}}{\lambda }} \right)\\ = 4c{\rm{os}}\left( {2\pi t + \dfrac{\pi }{6} - \dfrac{{2\pi .16}}{{32}}} \right)\\ = 4c{\rm{os}}\left( {2\pi t - \dfrac{{5\pi }}{6}} \right)cm\end{array}$

Phương trình vận tốc tại M:

 ${v_M} = {u_M}' =  - 8\pi \sin \left( {2\pi t - \dfrac{{5\pi }}{6}} \right)cm/s$

=> Vận tốc tại M tại thời điểm $t{\rm{ }} = {\rm{ }}2,5s$:

${v_{{M_{t = 2,5s}}}} =  - 8\pi \sin \left( {2\pi .2,5 - \dfrac{{5\pi }}{6}} \right) =  - 8\pi \sin \left( {\dfrac{{25\pi }}{6}} \right) =  - 4\pi cm/s$

+ Ta có, bước sóng:  $\lambda  = \dfrac{v}{f} = \dfrac{{0,3}}{{12}} = 0,025m = 2,5cm$

+ Độ lệch pha giữa hai điểm P và Q là: $\Delta \varphi  = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{2\pi .6,25}}{{2,5}} = 5\pi  = 4\pi  + \pi$

Vẽ trên vòng tròn lượng giác ta được:

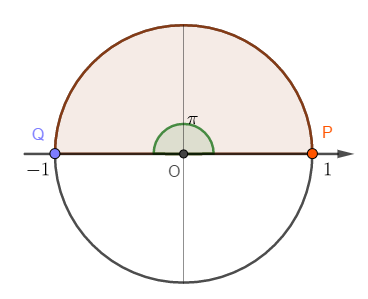
Từ vòng tròn lượng giác, ta có li độ tại Q là $- 1cm$

Ta có: $\lambda  = \dfrac{v}{f} = \dfrac{{200}}{{16}} = 12,5cm$

Chu kì: $T = \dfrac{1}{f} = \dfrac{1}{{16}}{\rm{s}}$

Độ lệch pha giữa hai điểm M và N là: $\Delta \varphi  = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{2\pi .21,875}}{{12,5}} = \dfrac{{7\pi }}{2} = 2\pi  + \dfrac{{3\pi }}{2}$

=> M và N dao động vuông pha nhau

Vì M gần nguồn sóng hơn => M nhanh pha hơn N 1 góc $\dfrac{{3\pi }}{2}$

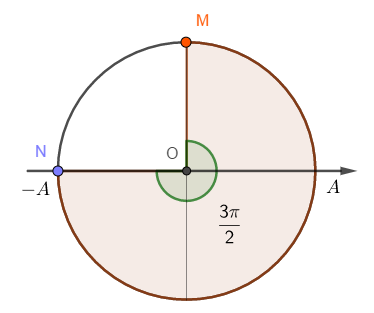
Tại thời điểm t: N đang ở biên âm, M đang ở VTCB theo chiều âm

=> Thời gian ngắn nhất điểm M hạ xuống thấp nhất (biên âm) là: $\Delta t = \dfrac{T}{4} = \dfrac{{\dfrac{1}{{16}}}}{4} = \dfrac{1}{{64}}s$

Ta có:

+ Điểm M ở vị trí cao nhất tức là biên dương.

+ Điểm N qua vị trí có li độ bằng $\dfrac{A}{2}$ và đang đi lên

Vẽ trên vòng tròn lượng giác, ta được:

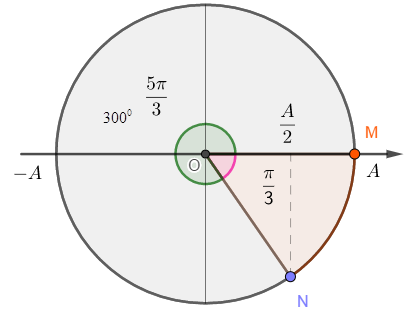
Ta có 2 trường hợp của góc lệch pha giữa M và N:

+ TH 1: M, N lệch pha nhau: $\Delta \varphi  = \dfrac{\pi }{3}$

$\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{\pi }{3}\\ \to \lambda  = 6\Delta d = 6.5 = 30cm\\ \to v = \lambda f = 30.15 = 450cm/s = 4,5m/s\end{array}$

M sớm pha hơn N => Sóng truyền từ M đến N

+ TH 2: M, N lệch pha nhau $\Delta \varphi  = \dfrac{{5\pi }}{3}$

$\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{5\pi }}{3}\\ \to \lambda  = \dfrac{6}{5}\Delta d = \dfrac{6}{5}.5 = 6cm\\ \to v = \lambda f = 6.15 = 90cm/s\end{array}$

Do N sớm pha hơn M

=> Sóng truyền từ N đến M

Ta có:

Độ lệch pha giữa hai điểm MN là: $\Delta \varphi  = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{2\pi \dfrac{\lambda }{3}}}{\lambda } = \dfrac{{2\pi }}{3}$

Giả sử dao động tại M sớm pha hơn dao động tại N.

Cách 1: Dùng phương trình sóng

Ta có thể viết:

$\begin{array}{l}{u_M} = Ac{\rm{os}}\omega t =  + 6cm{\rm{                (1)}}\\{u_N} = Ac{\rm{os}}\left( {\omega t - \dfrac{{2\pi }}{3}} \right) =  - 6cm{\rm{    (2)}}\end{array}$

Lấy (1) + (2), ta được:

$\begin{array}{l}{u_M} + {u_N} = 0 = Ac{\rm{os}}\omega t + Ac{\rm{os}}\left( {\omega t - \dfrac{{2\pi }}{3}} \right)\\ \leftrightarrow 2Ac{\rm{os}}\dfrac{\pi }{3}{\rm{cos}}\left( {\omega t - \dfrac{\pi }{3}} \right) = 0 \to \omega t - \dfrac{\pi }{3} = \dfrac{\pi }{2} + k\pi \\ \to \omega t = \dfrac{{5\pi }}{6} + k\pi \end{array}$

Thay vào (1), ta được: $Ac{\rm{os}}\left( {\dfrac{{5\pi }}{6} + k\pi } \right) = 2$

Do A > 0,

$\begin{array}{l}Ac{\rm{os}}\left( {\dfrac{{5\pi }}{6} - \pi } \right) = 6\\ \to Ac{\rm{os}}\left( { - \dfrac{\pi }{6}} \right) = 6 \to A = 4\sqrt 3 cm\end{array}$

Cách 2: Sử dụng vòng tròn lượng giác

Xác định tọa độ N, M trên vòng tròn lượng giác, ta được:

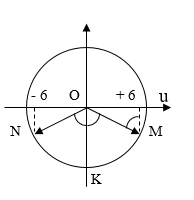
Từ vòng tròn lượng giác, ta có:

$\begin{array}{l}\angle NOK = \angle KOM = \dfrac{{\Delta \varphi }}{2} = \dfrac{\pi }{3}\\ \to {\rm{A}}\sin \dfrac{\pi }{3} = 6cm \to A = 4\sqrt 3 cm\end{array}$

+ Ta có:

$\begin{array}{l}{u_O} = A\sin \left( {\dfrac{{2\pi }}{T}t + \dfrac{\pi }{3}} \right)(cm)\\ \to {u_M}{\rm{ = Asin}}\left( {\dfrac{{2\pi }}{T}t + \dfrac{\pi }{3} - \dfrac{{2\pi x}}{\lambda }} \right)cm\end{array}$

+ Thay $t = \dfrac{T}{2}$ và $x = \dfrac{\lambda }{3}$ vào phương trình dao động tại M, ta được:

$\begin{array}{l}{u_M}{\rm{ = Asin}}\left( {\dfrac{{2\pi }}{T}t + \dfrac{\pi }{3} - \dfrac{{2\pi x}}{\lambda }} \right)\\ \leftrightarrow {\rm{Asin}}\left( {\dfrac{{2\pi }}{T}\dfrac{T}{2} + \dfrac{\pi }{3} - \dfrac{{2\pi \dfrac{\lambda }{3}}}{\lambda }} \right) = 3\\ \to A\sin \left( {\dfrac{{2\pi }}{3}} \right) = 3\\ \to A = 2\sqrt 3 cm\end{array}$

Ta có:              

- Phương trình sóng tại O: ${u_0} = Ac{\rm{os}}\left( {\omega t - \dfrac{\pi }{2}} \right)cm$

- Phương trình sóng tại M: ${u_M} = Ac{\rm{os}}\left( {\omega t - \dfrac{\pi }{2} - \dfrac{{2\pi d}}{\lambda }} \right)cm$

Tại $t = 2T$ và $d = \dfrac{\lambda }{8}$

$\begin{array}{l}{u_M} = Ac{\rm{os}}\left( {\dfrac{{2\pi }}{T}2T - \dfrac{\pi }{2} - \dfrac{{2\pi \dfrac{\lambda }{8}}}{\lambda }} \right) =  - 3cm\\ \to Ac{\rm{os}}\left( {\dfrac{{13\pi }}{4}} \right) =  - 3\\ \to A = 3\sqrt 2 cm\end{array}$

+ Từ phương trình sóng, ta có: $\dfrac{{2\pi x}}{\lambda } = \dfrac{{\pi x}}{4} \to \lambda  = 8m$

+ Độ lệch pha giữa 2 điểm M, N là: $\Delta \varphi  = \dfrac{{2\pi x}}{\lambda } = \dfrac{{2\pi .6}}{8} = \dfrac{{3\pi }}{2}$

Ta có, sóng truyền từ M đến N

=> M nhanh pha hơn N một góc $\dfrac{{3\pi }}{2}$

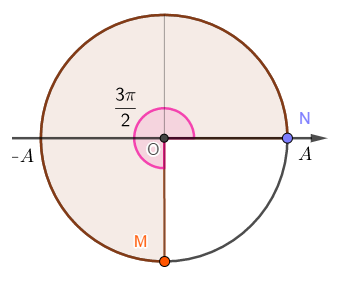
=> Khi M đi qua vị trí cân bằng theo chiều dương thì N đi qua vị trí biên dương

+ Ta có: $u = a\sin \left( {4\pi t + \frac{\pi }{4} - \frac{{2\pi x}}{3}} \right)\left( {m,s} \right)$

=> Sóng chạy theo chiều dương của trục x

$\frac{{2\pi x}}{\lambda } = \frac{{2\pi x}}{3} \to \lambda  = 3m$

+ Vận tốc truyền sóng: $v = \lambda f = \lambda \frac{\omega }{{2\pi }} = 3.\frac{{4\pi }}{{2\pi }} = 6m/s$

+ Tần số góc: $\omega  = 2\pi f = 2\pi .60 = 120\pi \left( {ra{\rm{d}}/s} \right)$

+ Góc quyét của M từ ${t_1}$ đến ${t_2}$ là: $\Delta \varphi  = \omega \Delta t = 120\pi .1,2 = 144\pi$

=> Li độ của M tại ${t_1}$ và ${t_2}$ cùng pha nhau

=> Tại ${t_2}$ M có li độ là $2cm$

Xác định tọa độ các điểm tại các thời điểm t₁ và t₂

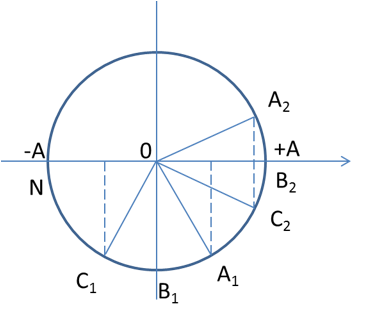
Từ vòng tròn lượng giác, ta có:

B quay góc ${90^0}$

=> Tại t₂ li độ B chính bằng biên độ

A, C cũng tương tự

Ta có:

$\begin{array}{l}\dfrac{{2,{4^2}}}{{{A^2}}} + \dfrac{{3,{2^2}}}{{{A^2}}} = 1\\ \to A = \sqrt {2,{4^2} + 3,{2^2}}  = 4mm\end{array}$

+ Biên độ sóng: $A = 3cm$

+ Bước sóng: $\lambda  = vT = 32.0,5 = 16cm$

+ Tần số góc: $\omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,5}} = 4\pi ra{\rm{d}}/s$

PT sóng tại M:

$\begin{array}{l}{u_M} = 3c{\rm{os}}\left( {4\pi t - \frac{{2\pi d}}{\lambda }} \right)\\ = 3c{\rm{os}}\left( {4\pi t - \frac{{2\pi .50}}{{16}}} \right)\\ = 3c{\rm{os}}\left( {4\pi t - \frac{{25\pi }}{4}} \right)\\ = 3c{\rm{os}}\left( {4\pi t - \frac{25\pi }{4}} \right)cm\end{array}$

+ Biên độ sóng: $A = 3cm$

+ Bước sóng: $\lambda  = vT = 32.0,5 = 16cm$

+ Tần số góc: $\omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,5}} = 4\pi ra{\rm{d}}/s$

PT sóng tại M:

$\begin{array}{l}{u_M} = 3c{\rm{os}}\left( {4\pi t - \frac{{2\pi d}}{\lambda }} \right)\\ = 3c{\rm{os}}\left( {4\pi t - \frac{{2\pi .50}}{{16}}} \right)\\ = 3c{\rm{os}}\left( {4\pi t - \frac{{25\pi }}{4}} \right)\\ = 3c{\rm{os}}\left( {4\pi t - \frac{\pi }{4}} \right)cm\end{array}$

PT sóng tại O: $u = ac{\rm{os}}\omega {\rm{t}}\left( {cm} \right)$

PT sóng tại M:

${u_M} = ac{\rm{os}}\left( {\omega t \pm \frac{{2\pi d}}{\lambda }} \right) = ac{\rm{os}}\left( {\omega t \pm \frac{{2\pi \frac{{2\lambda }}{3}}}{\lambda }} \right) = ac{\rm{os}}\left( {\omega t \pm \frac{{4\pi }}{3}} \right)$

Tại thời điểm $t{\rm{ }} = {\rm{ }}0,5T$ thì $u = 3cm$

$\begin{array}{l}{u_M} = ac{\rm{os}}\left( {\omega \frac{T}{2} \pm \frac{{4\pi }}{3}} \right) = ac{\rm{os}}\left( {\frac{{2\pi }}{T}.\frac{T}{2} \pm \frac{{4\pi }}{3}} \right)\\ = ac{\rm{os}}\left( {\frac{{2\pi }}{T}.\frac{T}{2} \pm \frac{{4\pi }}{3}} \right) = 3cm\\ \leftrightarrow ac{\rm{os}}\left( {\pi  \pm \frac{{4\pi }}{3}} \right) = 3cm\\ \to a = 6cm\end{array}$

=> Phương trình sóng tại M: ${u_M} = 6\cos (\omega t - \frac{{4\pi }}{3})cm$

Bước sóng: $\lambda  = vT = v\frac{{2\pi }}{\omega } = 1,2\frac{{2\pi }}{{4\pi }} = 0,6m$

Sóng truyền từ N đến M, ta có phương trình sóng tại M là:

$\begin{array}{l}{u_M} = 0,2c{\rm{os}}\left( {4\pi t - \frac{{2\pi d}}{\lambda }} \right)\\ = 0,2c{\rm{os}}\left( {4\pi t - \frac{{2\pi 0,5}}{{0,6}}} \right)\\ = 0,2c{\rm{os}}\left( {4\pi t - \frac{{5\pi }}{3}} \right)m\end{array}$

+ Bước sóng: $\lambda  = vT = v\frac{{2\pi }}{\omega } = 6\frac{{2\pi }}{{5\pi }} = 2,4m$

+ Do M nằm trước O, ta có phương trình dao động của M là:

$\begin{array}{l}{u_M} = 6c{\rm{os}}\left( {5\pi t + \frac{\pi }{3} + \frac{{2\pi d}}{\lambda }} \right)\\ = 6c{\rm{os}}\left( {5\pi t + \frac{\pi }{3} + \frac{{2\pi 0,5}}{{2,4}}} \right)\\ = 6c{\rm{os}}\left( {5\pi t + \frac{{3\pi }}{4}} \right)cm\end{array}$

Li độ của phần tử sóng là:

u = 5cos(8πt-0,04πx) = 5cos(8π.3-0,04π.25) = -5 (cm)

Ở thời điểm t₀, tốc dộ dao động của các phần tử tại B và C đều bằng v₀. còn phần tử tại trung điểm D của BC đang ở biên biểu diễn trên vòng tròn lượng giác ta được

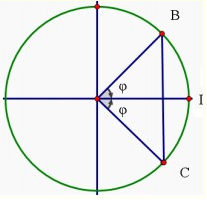
Ở thời điểm t₁, vận tốc của các phần tử tại B và C có giá trị đều bằng v₀ khi biểu diễn trên đường tròn lượng giác ta có

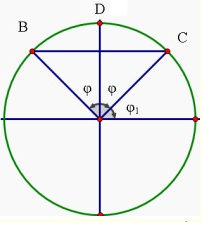
Do $\widehat {COB} = const$ và vận tốc tại t₀ và t₁  bằng nhau nên $\varphi  = {\varphi _1} = \dfrac{\pi }{4}$

Tại t₁ vận tốc tại D đạt giá trị cực đại nên  $\left\{ \begin{array}{l}\cos \varphi  = \dfrac{{{v_1}}}{{{v_{max}}}}\\\sin \varphi   =  \dfrac{{{v_2}}}{{{v_{max}}}}\end{array} \right. =  > {v_{max}} = \sqrt {v_0^2 + v_0^2}  = \sqrt 2 {v_0}$