Một sóng cơ hình sin truyền theo trục Ox. Phương trình dao động của một phần tử trên Ox là \(u = 2\cos 10t\left( {mm} \right)\). Biên độ của sóng là
Ta có phương trình dao động sóng: \(u = 2cos10t\left( {mm} \right)\)
=> Biên độ của sóng: \(A = 2mm\)
Một sóng ngang truyền trên sợi dây rất dài với phương trình sóng \(u = A\cos \left( {20\pi t - \frac{\pi }{{10}}x} \right)\) (\(x\) tính bằng \({\rm{cm}},t\) tính bằng \({\rm{s}})\). Bước sóng trên sợi dây là
Đối chiếu phương trình sóng với phương trình tổng quát, ta có:
\(\frac{{2\pi x}}{\lambda } = \frac{\pi }{{10}}x \Rightarrow \lambda = 20\,\left( {cm} \right)\)
Một sóng cơ dao động có bước sóng là \(\lambda \). Khoảng cách giữa 5 ngọn sóng liên tiếp là:
Ta có: Khoảng cách giữa n ngọn sóng liên tiếp là: n - 1 bước sóng
=> Khoảng cách giữa 5 ngọn sóng liên tiếp là \(4\lambda \)
Một người ngồi ở bờ biển quan sát thấy khoảng cách giữa bảy ngọn sóng liên tiếp bằng \(21m\). Bước sóng là:
Ta có, khoảng cách giữa bảy ngọn sóng liên tiếp là:
\(\begin{array}{l}6\lambda = 21m\\ \to \lambda = \frac{{21}}{6} = 3,5m\end{array}\)
Một người ngồi ở bờ biển quan sát thấy khoảng cách giữa năm ngọn sóng liên tiếp bằng 10m. Ngoài ra, người đó đếm được 10 ngọn sóng đi qua trước mặt trong \(27s\). Chu kì dao động của nước biển là:
Ta có, khoảng cách giữa năm ngọn sóng liên tiếp là: \(4\lambda = 10m \to \lambda = 2,5m\)
+ \(10\) ngọn sóng đi qua trước mặt tương đương với \(9\) bước sóng hay \(9\) chu kì dao động
Ta suy ra: \(9T = 27s \to T = 3s\)
Biểu thức nào sau đây là sai?
Ta có: \(\lambda = \frac{v}{f} = vT\)
=> Các phương án:
+ A, B, C – đúng
+ D – sai vì: \(\lambda = \frac{v}{f}\)
Một sóng truyền trong một môi trường với vận tốc \(120m/s\) và có bước sóng \(2m\). Tần số của sóng đó là:
Ta có: \(\lambda = \frac{v}{f} \to f = \frac{v}{\lambda } = \frac{{120}}{2} = 60Hz\)
Tại một điểm trên mặt chất lỏng có một nguồn dao động với tần số \(60{\rm{ }}Hz\), tạo ra sóng ổn định trên mặt chất lỏng. Xét \(6\) gợn lồi liên tiếp trên một phương truyền sóng ở về một phía so với nguồn, gợn thứ nhất cách gợn thứ sáu \(0,5m\). Tính tốc độ truyền sóng trên mặt chất lỏng:
Ta có:
+ Khoảng cách giữa \(6\) gợn lồi (ngọn sóng) là: \(5\lambda = 0,5m \to \lambda = 0,1m\)
+ Ta có: \(\lambda = \dfrac{v}{f} \to v = \lambda f = 0,1.60 = 6m/s\)
Một sóng ngang truyền theo chiều dương trục Ox, có phương trình sóng là \(u = 2cos\left( {4t - \dfrac{{\pi x}}{4}} \right)\); trong đó u và x tính bằng cm, t tính bằng s. Sóng này có bước sóng là:
Ta có:
\(\begin{array}{l}\Delta \varphi = \dfrac{{2\pi x}}{\lambda } = \dfrac{{\pi x}}{4}\\ \to \lambda = 2.4 = 8cm\end{array}\)
Một sóng hình sin truyền trên một sợi dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng:
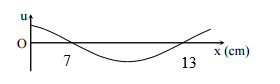
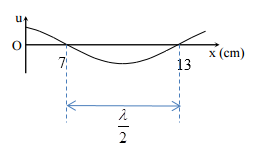
Từ đồ thị,
Ta có: \(\frac{\lambda }{2} = 13 - 7 = 6cm \to \lambda = 12cm\)
Một nguồn phát sóng dao động theo phương trình \(u = ac{\rm{os4}}\pi {\rm{t}}\) (cm). Trong khoảng thời gian 2s sóng truyền đi được quãng đường bằng bao nhiêu lần bước sóng?
Ta có: \(T = \frac{{2\pi }}{{4\pi }} = 0,5s\)
\(2s = 4.0,5 = 4T\)
=> Quãng đường sóng truyền đi trong \(2s\) bằng \(4\) lần bước sóng
Biểu thức nào sau đây xác định độ lệch pha của dao động tại tại hai điểm M và N. Biết M, N cách nhau một khoảng d trên phương truyền sóng và sóng cơ học có bước sóng \(\lambda \)?
Độ lệch pha của hai dao động tại hai điểm M và N là: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda }\)
Một nguồn dao động điều hoà với chu kỳ \(0,2s\). Vận tốc truyền sóng bằng \(120cm/s\). Hai điểm nằm trên cùng một phương truyền sóng và cách nhau \(3cm\), có độ lệch pha:
Ta có:
+ Bước sóng: \(\lambda = vT = 120.0,2 = 24cm\)
+ Độ lệch pha của hai dao động tại hai điểm là: \(\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi 3}}{{24}} = \dfrac{\pi }{4}\left( {rad} \right)\)
Sóng cơ có tần số \(120Hz\) truyền trong môi trường với vận tốc \(180m/s\). Ở cùng một thời điểm, hai điểm gần nhau nhất trên một phương truyền sóng có dao động cùng pha với nhau, cách nhau:
+ Ta có: Khoảng cách giữa hai điểm gần nhau nhất trên một phương truyền sóng dao động cùng pha với nhau là 1 bước sóng.
+ Lại có bước sóng: \(\lambda = \frac{v}{f} = \frac{{180}}{{120}} = 1,5m\)
Một sóng ngang truyền trên sợi dây đàn hồi rất dài với tần số \(50Hz\). Người ta thấy hai điểm A, B trên sợi dây cách nhau \(0,2m\) dao động cùng pha và trên đoạn dây AB có hai điểm khác dao động ngược pha với A. Tốc độ truyền sóng trên dây là:
2 điểm A, B dao động cùng pha và trên AB có 2 điểm khác dao động ngược pha với A.
\( \to AB = 2\lambda = 0,2m \to \lambda = 0,1m\)
Ta có tốc độ truyền sóng: \(v = \lambda f = 0,1.50 = 5m/s = 500cm/s\)
Một sóng có tần số \(120Hz\) và tốc độ lan truyền \(72m/s\). Hỏi hai điểm gần nhất trên phương truyền sóng cách nhau một khoảng bao nhiêu để giữa chúng có độ lệch pha \(\frac{\pi }{2}\)?
Bước sóng: \(\lambda = \frac{v}{f} = \frac{{72}}{{120}} = 0,6m\)
Để độ lệch pha giữa 2 điểm gần nhất là \(\frac{\pi }{2}\)
\( \leftrightarrow \Delta \varphi = \frac{{2\pi d}}{\lambda } = \frac{\pi }{2} \to d = \frac{\lambda }{4} = \frac{{0,6}}{4} = 0,15m = 15cm\)
Một sợi dây đàn hồi rất dài có đầu \(A\) dao động với tần số \(f\) và theo phương vuông góc với sợi dây. Biên độ dao động là \(5cm\), vận tốc truyền sóng trên đây là \(2m/s\). Xét một điểm M trên dây và cách A một đoạn \(12cm\), người ta thấy M luôn luôn dao động lệch pha với A một góc \(\Delta \varphi = (2k + 1)\dfrac{\pi }{2}\) với \(k{\rm{ }} = {\rm{ }}0, \pm 1, \pm 2\). Tính bước sóng \(\lambda \)? Biết tần số \(f\) có giá trị trong khoảng từ \(20{\rm{ }}Hz\) đến \(26{\rm{ }}Hz\).
Độ lệch pha:
\(\begin{array}{l}\Delta \varphi = (2k + 1)\dfrac{\pi }{2} = \dfrac{{2\pi d}}{\lambda }\\ \to f = \left( {2k + 1} \right)\dfrac{v}{{4d}}\end{array}\)
Mặt khác: \(20{\rm{ }}Hz < f < 26{\rm{ }}Hz\)
\(\begin{array}{l} \to 20 < f = \left( {2k + 1} \right)\dfrac{v}{{4d}} < 26\\ \leftrightarrow 20 < \left( {2k + 1} \right)\dfrac{2}{{4.0,12}} < 26\\ \to 1,9 < k < 2,62\\ \to k = 2\\ \to f = \left( {2.2 + 1} \right)\dfrac{2}{{4.0,12}} = \dfrac{125}{6}H{\rm{z}}\\ \to \lambda = \dfrac{v}{f} = \dfrac{2}{\dfrac{125}{6}} = 0,096m = 9,6cm\end{array}\)
Một sóng ngang có chu kì \(T = 0,2s\) truyền trong một môi trường đàn hồi có tốc độ \(2m/s\). Xét trên phương truyền sóng Ox, vào một thời điểm nào đó một điểm M nằm tại đỉnh sóng thì ở sau M theo chiều truyền sóng, cách M một khoảng từ \(82cm\) đến \(120cm\) có điểm N đang từ vị tri cân bằng đi lên đỉnh sóng . Khoảng cách MN là:
Vẽ trên vòng tròn lượng giác thì lúc M ở góc \({0^0}\) \(\left( {x = A} \right)\) thì N ở góc \( - \dfrac{\pi }{2}\)
Sóng truyền từ M đến N \( \Rightarrow \) M sớm pha hơn N một góc \(\dfrac{\pi }{2}\)
\( \Rightarrow MN = \dfrac{\lambda }{4} + k\lambda = 0,1 + 0,4k\)
Có
\(\begin{array}{l}0,82 < MN < 1,2\\ \Leftrightarrow 0,82 < 0,1 + 0,4k < 1,2\\ \Leftrightarrow 1,8 < k < 2,75\\ \Rightarrow k = 2\end{array}\)
\( \Rightarrow MN = \dfrac{\lambda }{4} + 2\lambda = \dfrac{{9\lambda }}{4} = 0,9m = 90cm\)
Một dây đàn hồi dài có đầu A dao động theo phương vuông góc với sợi dây. Tốc độ truyền sóng trên dây là \(2{\rm{ }}m/s\). Xét một điểm M trên dây và cách A một đoạn \(40{\rm{ }}cm\), người ta thấy M luôn luôn dao động lệch pha so với A một góc \(\Delta \varphi = \left( {k + \dfrac{1}{2}} \right)\pi \) với k là số nguyên. Tính tần số, biết tần số \(f\) có giá trị trong khoảng từ \(8{\rm{ }}Hz\) đến \(11{\rm{ }}Hz\).
+ Độ lệch pha giữa M và A:
\(\begin{array}{l}\Delta \varphi = \dfrac{{2\pi d}}{\lambda } = \dfrac{{2\pi d}}{{\dfrac{v}{f}}}\\ \Rightarrow \dfrac{{2\pi df}}{v} = \left( {k + \dfrac{1}{2}} \right)\pi \\ \Rightarrow f = \left( {k + \dfrac{1}{2}} \right)\dfrac{v}{{2d}}\\ = \left( {k + \dfrac{1}{2}} \right)\dfrac{2}{{2.0,4}} = 2,5\left( {k + 0,5} \right)Hz\end{array}\)
+ Do:
\(\begin{array}{l}8Hz \le f \le 13Hz\\ \to 8 \le 2,5\left( {k + 0,5} \right) \le 11\\ \leftrightarrow 2,7 \le k \le 3,9\\ \to k = 3\\ \to f = 2,5\left( {3 + 0,5} \right) = 8,75Hz\end{array}\)
Đề thi THPT QG - 2020
Một sóng cơ hình sin có tần số \(f\) lan truyền trong một môi trường với bước sóng \(\lambda \). Bước sóng của sóng này là
Bước sóng: \(\lambda = \dfrac{v}{f}\)

