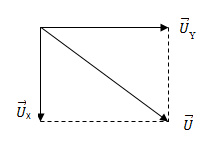
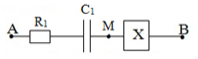
Mạch điện xoay chiều như hình vẽ. Hộp X chứa các phần tử R2, L, C2 mắc nối tiếp. Đặt điện áp xoay chiều vào hai đầu mạch AB có tần số 50 Hz và giá trị hiệu dụng 220 V thì cường độ dòng điện trong mạch có giá trị hiệu dụng \(\sqrt 2 \,\,\left( A \right)\). Biết \({R_1} = 40\sqrt 2 \,\,\Omega \). Tại thời điểm t(s) cường độ dòng điện I = 2A, ở thời điểm \(\left( {t + \dfrac{1}{{600}}} \right)s\), điện áp \({u_{AB}} = 0\left( V \right)\) và đang giảm. Công suất của đoạn mạch MB nhận giá trị nào sau đây
Cường độ dòng điện hiệu dụng và cực đại: \(\left\{ \begin{array}{l}I = \sqrt 2 A\\{I_0} = 2A\end{array} \right.\)
Điện áp hiệu dụng giữa hai đầu đoạn mạch AB: \(U = 220V\)
Tại thời điểm t(s) cường độ dòng điện là \(i = 2A = {I_0}\), ở thời điểm \(\left( {t + \dfrac{1}{{600}}} \right)s\) điện áp \({u_{AB}} = 0\,\left( V \right)\)và đang giảm.
Góc quét được trong thời gian \(\dfrac{1}{{600}}s\) là:
\(\alpha = \omega .\Delta t = 100\pi .\dfrac{1}{{600}} = \dfrac{\pi }{6}rad\)
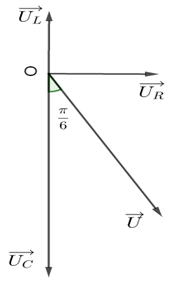
Biểu diễn trên VTLG cường độ dòng điện chạy trong mạch và điện áp giữa hai đầu đoạn mạch AB tại thời điểm \(\left( {t + \dfrac{1}{{600}}} \right)s\) như sau:
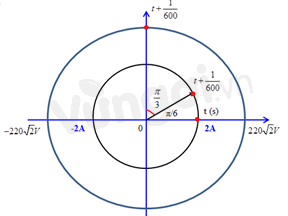
Từ VTLG ta xác định được độ lệch pha giữa u và i là: \(\varphi = \dfrac{\pi }{3}rad\)
Công suất tiêu thụ của đoạn mạch AB là:
\({P_{AB}} = U.I.\cos \varphi = 220.\sqrt 2 .\cos \dfrac{\pi }{3} = 110\sqrt 2 \,\left( {\rm{W}} \right)\)
Công suất tiêu thụ của đoạn mạch AM là:
\({P_{AM}} = {I^2}{R_1} = {\left( {\sqrt 2 } \right)^2}.40\sqrt 2 = 80\sqrt 2 \,\left( {\rm{W}} \right)\)
Công suất của đoạn mạch MB là:
\({P_{MB}} = {P_{AB}} - {P_{AM}} = 110\sqrt 2 - 80\sqrt 2 = 30\sqrt 2 \,\left( {\rm{W}} \right)\)
Đặt điện áp xoay chiều hiệu dụng U vào hai đầu một hộp đen X thì dòng điện trong mạch có cường độ hiệu dụng là 0,25A và sớm pha π/2 so với điện áp hai đầu hộp đen X. Cũng đặt điện áp đó vào hai đầu hộp đen Y thì dòng điện trong mạch vẫn có cường độ hiệu dụng là 0,25A nhưng cùng pha với điện áp hai đầu đoạn mạch. Nếu đặt điện áp trên vào hai đầu đoạn mạch gồm X và Y mắc nối tiếp thì cường độ hiệu dụng của dòng điện trong đoạn mạch là:
- Đặt điện áp xoay chiều hiệu dụng U vào hai đầu một hộp đen X: \({Z_X} = \frac{U}{{0,25}} = 4U\)
- Cũng đặt điện áp đó vào hai đầu hộp đen Y: \({Z_Y} = \frac{U}{{0,25}} = 4U\)
- Đặt điện áp trên vào hai đầu đoạn mạch gồm X và Y mắc nối tiếp:
Ta có: \(Z = \sqrt {Z_X^2 + Z_Y^2} = \sqrt {{{\left( {4U} \right)}^2} + {{\left( {4U} \right)}^2}} = 4\sqrt 2 U \Rightarrow I = \frac{U}{Z} = \frac{U}{{4\sqrt 2 U}} = \frac{{\sqrt 2 }}{8}A\)
Đoạn mạch AB chỉ gồm một phần tử chưa xác định (có thể là R,L,hoặc C). Trong đó ta xác định được biểu thức \(i{\rm{ }} = {\rm{ }}4cos100\pi t{\rm{ }}A\) và biểu thức \(u{\rm{ }} = {\rm{ }}40{\rm{ }}cos\left( {{\rm{ }}100\pi t{\rm{ }} + {\rm{ }}\pi /2} \right){\rm{ }}V\) . Hãy xác định phần tử trên? Và tính giá trị của nó khi đó?
Do hiệu điện thế giữa 2 đầu đoạn mach sớm pha hơn cường độ dòng điện \(\pi /{\rm{ }}2\) và trong mạch chỉ có 1 phần tử
=> Trong mạch chỉ có cuộn dây thuần cảm.
\( \to {Z_L} = \frac{U}{I} = 10 \to L = \frac{1}{{10\pi }}H.\)
Đoạn mạch AB chỉ gồm một phần tử chưa xác định (có thể là R,L,hoặc C). Trong đó ta xác định được biểu thức \(i{\rm{ }} = {\rm{ }}4cos100\pi t{\rm{ }}A\)và biểu thức \(u{\rm{ }} = {\rm{ }}40{\rm{ }}cos\left( {{\rm{ }}100\pi t - \pi /2} \right){\rm{ }}V\)Hãy xác định phần tử trên? Và tính giá trị của nó khi đó?
Do hiệu điện thế giữa 2 đầu đoạn mach trễ pha hơn cường độ dòng điện \(\pi /2\) và trong mạch chỉ có 1 phần tử
=> Trong mạch chỉ có tụ điện.
\( \to {Z_C}{\rm{ }} = \frac{U}{I} = 10 \to C = \frac{{{{10}^{ - 3}}}}{\pi }F\)
Đoạn mạch AB chỉ gồm một phần tử chưa xác định (có thể là R,L,hoặc C). Trong đó ta xác định được biểu thức \(i{\rm{ }} = {\rm{ }}4cos100\pi t{\rm{ }}A\) và biểu thức \(u{\rm{ }} = {\rm{ }}40{\rm{ }}cos({\rm{ }}100\pi t{\rm{ }})V\) . Hãy xác định phần tử trên? Và tính giá trị của nó khi đó? Tính công suất của mạch điện?
Do hiệu điện thế giữa 2 đầu đoạn mach cùng pha với cường độ dòng điện và trong
mạch chỉ có 1 phần tử
=> Trong mạch chỉ có điện trở thuần.
\( \to R = \frac{U}{I} = 10 \to R{\rm{ }} = 10\Omega \)
Đoạn mạch AB chứa hai phần tử trong ba phần tử( R,L,C) nhưng chưa được xác định. Biết rẳng biểu thức dòng điện trong mạch là \(i{\rm{ }} = {\rm{ }}4cos({\rm{ }}100\pi t{\rm{ }} + \pi /3)(A)\). Và biểu thức cường độ dòng điện trong mạch là \(u{\rm{ }} = {\rm{ }}200cos({\rm{ }}100\pi t{\rm{ }} + \pi /6)(V)\) . Hãy xác định hai phần tử trên? Tính công suất trong mạch?
Do u trễ pha hơn i 1 góc 0 < π/6 < π/2 => Trong mạch gồm tụ điện và điện trở thuần .
\( \to Z = \frac{U}{I} = \sqrt {{R^2} + Z_C^2} = 50\Omega \) (1)
Lại có : \(\tan \frac{\pi }{6} = \frac{{Z{}_C}}{R} \to R = \sqrt 3 {Z_C}\) (2)
Từ (1) và (2) =>\(R = 25\sqrt 3 \Omega ;{Z_C} = 25\Omega \)
\( \to P = {I^2}R = 8.25\sqrt 3 = 200\sqrt 3 {\rm{W}}\)
Đoạn mạch AB chứa hai phần tử trong ba phần tử( R,L,C) nhưng chưa được xác định. Biết rẳng biểu thức dòng điện trong mạch là \(i{\rm{ }} = {\rm{ }}4cos({\rm{ }}100\pi t{\rm{ }} - \pi /3)(A)\) . Và biểu thức cường độ dòng điện trong mạch là \(u{\rm{ }} = {\rm{ }}200cos({\rm{ }}100\pi t{\rm{ }} + \pi /6)(V)\) . Hãy xác định hai phần tử trên? Và tính công suất trong mạch?
Do hiệu điện thế giữa 2 đầu đoạn mach sớm pha hơn cường độ dòng điện \(\pi /2\) và trong mạch chỉ có 2 phần tử
=> Trong mạch chỉ có cuộn dây thuần cảm và tụ điện.
=> P = 0
Đoạn mạch AB gồm hai phần tử X,Y trong đó UX = 50 V, UY = 20 V và giá trị hiệu điện thế UAB = 30 V. vậy phần tử X,Y là gì?
UAB = Ux + (-Uy)
=> x,y phải ngược pha
=> X,Y là phần tử L,C
Đoạn mạch AB gồm hai phần tử X,Y trong đó UX = 40 V, UY = 30 V và giá trị hiệu điện thế UAB = 50 V và u nhanh pha hơn i. Vậy phần tử X,Y là gì?
UAB2 = Ux2 + Uy2
=> Hiệu điện thế 2 đầu phần tử X và Y vuông pha với nhau
=> X,Y có thể là 2 phần tử R,L hoặc R,C.
Do u nhanh pha hơn i nên X,Y là 2 phần tử R,L
Cho mạch điện gồm hai phần tử x,y mắc nối tiếp, trong đó: x,y có thể là R,L hoặc C. Cho biết hiệu điện thế giữa hai đầu đoạn mạch \({u_{AB}} = {\rm{ }}200\sqrt 2 cos100\pi t{\rm{ }}V\) và \(i = 2\sqrt 2 cos(100\pi t{\rm{ }} - \pi /6)(A)\) . x,y là phần tử gì?
Do u sớm pha hơn i 1 góc \(0 < \pi /6 < \pi /2{\rm{ }}\)
=> Trong mạch L và R
Mạch điện X chưa xác định, qua thực nghiệm thấy được dòng điện trong mạch \(i{\rm{ }} = 5cos({\rm{ }}100\pi t){\rm{ }}A\) , và hiệu điện thế trong mach \(u{\rm{ }} = 100cos({\rm{ }}100\pi t){\rm{ }}V\) . Mach X có thể gồm phần tử gì?
Do u và i cùng pha nên trong mạch chỉ có điện trở R hoặc mạch RLC cộng hưởng
Đoạn mạch X chỉ gồm tụ điện, để dòng điện trong mạch chậm pha hơn u một góc \(\pi /3\) cần ghép nối tiếp X với Y. Xác định phần tử Y
Do ban đầu cường độ dòng điện sớm pha hơn hiệu điện thế hai đầu đoạn mạch nên để hiệu điện thế sớm pha hơn cường độ dòng điện thì phải mắ thêm 1 cuộn cảm sao cho ZL >Zc.
Để u sớm pha hơn i 1 góc π/3 thì phải mắc thêm 1 điện trở sao cho: \(\tan \frac{\pi }{3} = \frac{{{Z_L} - {Z_C}}}{R}\)
=> Y gồm điện trở R và cuộn dây có hệ số tự cảm L
Mạch X có hai phần tử, u nhanh pha hơn \(i\), Ghép X với Y thì thấy trong mạch có biểu thức \(i = \dfrac{u}{Z}\). Hãy xác định phần tử có thể có của Y?
Do u nhanh pha hơn i nên trong mạch X có R,L .
Mặt khác, khi nối tiếp với đoạn mạch Y thì \(i = \dfrac{u}{Z}\)
=> i cùng pha vơi u
=> Trong mạch xảy ra hiện tượng cộng hưởng
=> Trong mạch Y có thể chứa phần tử C sao cho \(Z_L=Z_C\) hoặc chứa R, C sao cho \(Z_L=Z_C\)
\(\to\) Phương án A, B đúng
Mạch điện gồm hai phần tử L,C trong đó \(L{\rm{ }} = {\rm{ }}1/\pi H\) và \(C{\rm{ }} = {\rm{ }}{10^{ - 3}}/6\pi F\) . Mắc nối tiếp đoạn mạch trên với phần tử X( X chỉ chứa 2 phần tử) và mắc vào mạng điện \(u{\rm{ }} = {\rm{ }}50cos\left( {{\rm{ }}100\pi t{\rm{ }} + {\rm{ }}\pi /3} \right)V\) , thì thấy công suất trong mạch là 25W và đang có hiện tượng cộng hưởng xảy ra. Xác định các phần tử X trên và tìm giá trị của nó?
\({Z_L} = \omega L = 100\Omega ;{Z_C} = \frac{1}{{\omega C}} = 60{\rm{ }}\Omega \)
Để xảy ra hiện tượng cộng hưởng thì trên đoạn mạch X phải có điện trở thuần R tu điện C' Sao cho
\(\begin{array}{*{20}{l}}{{Z_{{C_0}}} = {\rm{ }}{Z_L} = 100\Omega \to {C_0}{\rm{ }} = \frac{{{{10}^{ - 4}}}}{\pi }F}\\{ \to C' = \frac{{{{10}^{ - 3}}}}{{4\pi }}F}\end{array}\)
Điện trở thuần: \(R = \frac{{{U^2}}}{P} = 50\Omega \)
Mạch điện X có hai phần tử ( trong ba phần tử R,L,C). mắc mạch điện trên vào mạng điện có \(u{\rm{ }} = {\rm{ }}50cos({\rm{ }}100\pi t{\rm{ }})(V)\) thì thấy dòng điện trong mạch có biểu thức \(i{\rm{ }} = {\rm{ }}2cos({\rm{ }}100\pi t{\rm{ }} - \pi /3)A.\) Xác định giá trị các phần tử trong mạch?
Do i trễ pha hơn u 1 góc \(\pi /3\) và trong mạch gồm 2 phần tử nên trong mạch có 2 phần tử R,L.
Ta có: \(\tan \frac{\pi }{3} = \frac{{{Z_L}}}{R} \to \sqrt 3 R = {Z_L}\) (1)
Mặt khác: Z = U/I = 25(2)
Từ (1) và (2) \( \to {Z_L} = 12,5\sqrt 3 ;R = 12,5\)
Cho mạch điện xoay chiều gồm điện biến trở mắc nối tiếp với hộp đen. Điện áp hai đầu mạch \({u_{AB}} = 200\sqrt 2 cos{\rm{ }}(100\pi t)(V)\), X chứa một phần tử (L hoặc C). Điều chỉnh R để công suất tiêu thụ trên mạch cực đại thì cường độ hiệu dụng trong mạch là \(\sqrt 2 A\) . Biết dòng điện trong mạch sớm pha hơn điện áp hai đầu mạch. Cấu tạo hộp X và giá trị của phần tử trong X là:
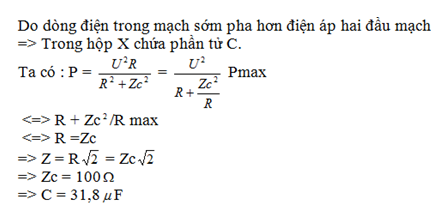
Cho mạch điện như hình vẽ. Đặt vào hai đầu đoạn \(AB\) một điện áp xoay chiều có chu kì \(T\), lúc đó \({Z_L} = \sqrt 3 r\). Hộp X chứa 2 trong ba phần tử điện trở \(R\), tụ điện có dung kháng \({Z_C}\), cuộn thuần cảm có độ tự cảm \({Z_{{L_0}}}\) ghép nối tiếp. Biết vào thời điểm \({t_1}\) thì điện áp tức thời \({u_{AM}}\) cực đại, đến thời điểm \(t = {t_1} + \dfrac{T}{3}\) thì điện áp tức thời \({u_{MB}}\) cực đại. Hộp X chứa các phần tử là
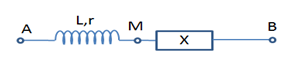
Ta có giản đồ vecto:
Ta có \(t = {t_1} + \dfrac{T}{3}\) nên \({U_{AM}}\) sớm pha góc \({120^0}\) so với \({U_{MB}}\)
Lệch pha nhau góc \({120^0}\) mà tại AM có \({Z_L} = \sqrt 3 r \Rightarrow {Z_L}\) lệch pha \({60^0}\) so với \(r\)
Nên \(AM\) sớm pha \({60^0}\) so với dòng điện.
Suy ra MB chậm pha \({120^0} - {60^0} = {60^0}\) so với dòng điện.
\( \Rightarrow X\) là R nối tiếp với C
\(\tan \left( { - {{60}^0}} \right) = \dfrac{{ - {Z_C}}}{R} \Rightarrow {Z_C} = \sqrt 3 R\)
Cho mạch điện như hình vẽ, X, Y là hai hộp kín, mỗi hộp chỉ chứa hai trong ba phần tử: điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Ampe kế có điện trở rất nhỏ, các vôn kế có điện trở rất lớn. Các vôn kế và ampe kế đo được cả dòng điện xoay chiều và một chiều. Ban đầu mắc hai điểm N, D vào hai cực của một nguồn điện không đổi thì vôn kế V2 chỉ 45V, ampe kế chỉ 1,5A. Sau đó đặt điện áp $u=120\cos 100\pi t\left( V \right)$ vào hai điểm M, D thì ampe kế chỉ 1A, hai vôn kế chỉ cùng một giá trị và uMN chậm pha $\frac{\pi }{2}$ so với uND. Khi thay tụ C trong mạch bằng tụ C’ thì điện áp hiệu dụng hai đầu tụ điện có giá trị lớn nhất UCmax. Giá trị UCmax gần giá trị nào nhất sau đây?
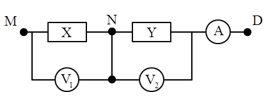
Khi mắc vào hai cực ND một điện áp không đổi → có dòng trong mạch với cường độ I = 1,5A
→ ND không thể chứa tụ (tụ không cho dòng không đổi đi qua) và ${{R}_{Y}}=\frac{45}{1,5}=30\left( \Omega \right)$
Mắc vào hai đầu đoạn mạch MD một điện áp xoay chiều thì uND sớm pha hơn uMN một góc 0,5π
→ X chứa điện trở RX và tụ điện C, Y chứa cuộn dây L và điện trở RY.
Mà V1 = V2 → UX = UY = 60V → ZX = ZY = 60Ω
Cảm kháng của cuộn dây là
${{Z}_{L}}=\sqrt{Z_{Y}^{2}-R_{Y}^{2}}=\sqrt{{{60}^{2}}-{{30}^{2}}}=30\sqrt{3}\Omega $
uMN sớm pha 0,5π so với uND và $\tan {{\varphi }_{Y}}=\frac{{{Z}_{L}}}{{{R}_{Y}}}=\frac{30\sqrt{3}}{30}=\sqrt{3}$ → φY = 600
→ φX = 300
$\to \left\{ \begin{align}& {{R}_{X}}=30\sqrt{3}\Omega \\& {{Z}_{C}}=30\Omega \\\end{align} \right.$
Điện áp hiệu dụng hai đầu MN bằng
${{V}_{1}}={{U}_{MN}}=\frac{U\sqrt{R_{X}^{2}+Z_{C}^{2}}}{\sqrt{{{\left( {{R}_{X}}+{{R}_{Y}} \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{60\sqrt{2}\sqrt{{{\left( 30\sqrt{3} \right)}^{2}}+Z_{C}^{2}}}{\sqrt{{{\left( 30\sqrt{3}+30 \right)}^{2}}+\left( 30\sqrt{3}-Z_{C}^{2} \right)}}$
Sử dụng bảng tính Mode →7 trên CASIO ta tìm được V1max có giá trị gần nhất với 75V.
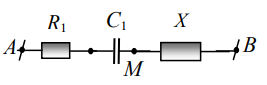
Đặt điện áp \(u = 220\sqrt 2 \cos \left( {100\pi t + \varphi } \right)\,\,\left( V \right)\) vào hai đầu đoạn mạch AB như hình bên. Biết hộp X là đoạn mạch có R, L, C mắc nối tiếp; cường độ dòng điện hiệu dụng trong mạch là \(2\sqrt 2 \,\,A\) và \({R_1} = 20\sqrt 2 \,\,\Omega \). Tại thời điểm t (s) cường độ dòng điện trong mạch bằng 4 A. Đến thời điểm \(t + \frac{1}{{300}}\,\,\left( s \right)\) thì điện áp u = 0 và đang giảm. Công suất của đoạn mạch X là
và \({R_1} = 20\sqrt 2 \,\,\Omega \). Tại thời điểm t (s) cường độ dòng điện trong mạch bằng 4 A. Đến thời điểm \(t + \frac{1}{{300}}\,\,\left( s \right)\) thì điện áp u = 0 và đang giảm. Công suất của đoạn mạch X là
Hai thời điểm lệch pha nhau là:
\(\Delta \varphi = \omega \Delta t = 100\pi .\frac{1}{{300}} = \frac{\pi }{3}\,\,\left( {rad} \right)\)
Ở thời điểm t, cường độ dòng điện trong mạch: I = 4 (A) = I0
Ta có vòng tròn lượng giác:
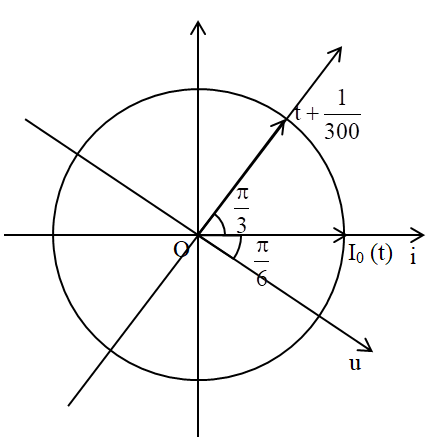
Tại thời điểm \(t + \frac{1}{{300}}s\), điện áp giữa hai đầu đoạn mạch bằng 0 và đang giảm
→ trục u lệch pha \(\frac{\pi }{6}\) so với trục i \( \Rightarrow \varphi = \frac{\pi }{6}\)
Công suất tiêu thụ của đoạn mạch là:
\(P = UI\cos \varphi = 220.2\sqrt 2 .cos\frac{\pi }{6} = 538,9\,\,\left( {\rm{W}} \right)\)
Công suất tiêu thụ của đoạn mạch X là:
\({P_X} = P - {I^2}{R_1} = 538,9 - {\left( {2\sqrt 2 } \right)^2}.20\sqrt 2 = 312,6\,\,\left( {\rm{W}} \right)\)
Đề thi thử THPT chuyên Lam Sơn - 2021
Cho dòng điện xoay chiều chạy qua đoạn mạch AB có sơ đồ như hình bên, trong đó L là cuộn cảm thuần và X là đoạn mạch xoay chiều. Khi đó, điện áp giữa hai đầu các đoạn mạch AN và MB có biểu thức điện áp lần lượt là \({u_{AN}} = 30\sqrt 2 co{\rm{s}}\left( {\omega t} \right)\) (V) và \({u_{MB}} = 40\sqrt 2 cos\left( {\omega t - \frac{\pi }{2}} \right)\left( V \right)\) . Điện áp hiệu dụng giữa hai đầu đoạn mạch AB có giá trị nhỏ nhất là
Ta có: \(\left\{ \begin{array}{l}{u_{AN}} = {u_L} + {u_X}\\{u_{MB}} = {u_C} + {u_X}\\{u_{AB}} = {u_{AN}} + {u_C}\end{array} \right.\)
Theo đề bài, ta có độ lệch pha giữa \({u_{AN}}\) và \({u_{MB}}\) là \(\frac{\pi }{2}\) hay nói cách khác \({u_{AN}} \bot {u_{MB}}\)
Vẽ trên giản đồ véctơ ta được:
Từ giản đồ, ta có \({U_{AB}} \ge OH \Rightarrow {U_{AB\min }} = OH\)
Sử dụng hệ thức lượng trong tam giác vuông \(O{U_{AN}}{U_{MB}}\) ta có:
\(\begin{array}{l}\frac{1}{{O{H^2}}} = \frac{1}{{U_{AN}^2}} + \frac{1}{{U_{MB}^2}} = \frac{1}{{{{30}^2}}} + \frac{1}{{{{40}^2}}} = \frac{1}{{576}}\\ \Rightarrow OH = 24 \Rightarrow {U_{AB\min }} = OH = 24V\end{array}\)