Một đoạn mạch điện xoay chiều RC có \(C=\displaystyle{{{{2.10}^{ - 4}}} \over {\sqrt 3 \pi }}F\), \(R = 50\Omega \). Đặt vào hai đầu mạch một điện áp xoay chiều thì dòng điện trong mạch có biểu thức là \(i = c{\rm{os}}\left( {100\pi t + \dfrac{\pi }{6}} \right)A\) . Biểu thức nào sau đây là của điện áp hai đầu đoạn mạch?
Cài đặt máy tính ở chế độ radian SHIFT MODE 4
Bấm máy tính MODE 2 (Chọn CMPLX)
Dung kháng của tụ điện \({Z_C} = \displaystyle{1 \over {\omega C}} = 50\sqrt 3 \Omega \)
Tổng trở của đoạn mạch \(\overline Z = R - i{Z_C} = 50 - 50\sqrt 3 i\)
Điện áp hai đầu đoạn mạch là \(\overline U = \overline I .\overline Z = \left( {1\angle \displaystyle{\pi \over 6}} \right)\left( {50 - 50\sqrt 3 i} \right)\) SHIFT 2 3 =
Ta đọc kết quả \(\overline U = 100\angle -\displaystyle{\pi \over 6}\)
Biểu thức điện áp hai đầu đoạn mạch là \(u = 100cos\left( {100\pi t - \dfrac{\pi }{6}} \right)V\)
Đặt một điện áp xoay chiều \(u = 60\sin \left( {100\pi t} \right)V\) vào hai đầu đoạn mạch gồm cuộn thuần cảm có hệ số tự cảm \(L = \dfrac{1}{\pi }H\) và tụ điện có điện dung \(C = \dfrac{{50}}{\pi }\mu F\) mắc nối tiếp. Biểu thức của cường độ dòng điện chạy trong mạch là:
Cài đặt máy tính ở chế độ radian SHIFT MODE 4
Bấm máy tính MODE 2 (Chọn CMPLX)
Cảm kháng của cuộn dây ZL = ωL = 100 Ω
Dung kháng của tụ điện ZC = 1/ωC = 200 Ω
Tổng trở của đoạn mạch là \(\overline Z = \left( {{Z_L} - {Z_C}} \right)i = (100-200)i= - 100i\)
Cường độ dòng điện trong mạch là \(\overline I = \dfrac{{\overline U }}{{\overline Z }} = \dfrac{{60\angle 0}}{{ - 100i}}\) SHIFT 2 3 =
Ta đọc kết quả \(\overline I = \dfrac{3}{5}\angle \dfrac{\pi }{2}\)
Biểu thức cường độ dòng điện trong mạch \(i = 0,6\sin \left( {100\pi t + \dfrac{\pi }{2}} \right)A\)
Một đoạn mạch gồm tụ \(C = \dfrac{{{{10}^{ - 4}}}}{\pi }F\)và cuộn dây thuần cảm có độ tự cảm \(L = \dfrac{2}{\pi}H\) mắc nối tiếp. Điện áp giữa 2 đầu cuộn cảm là \({u_L} = 100\sqrt 2 cos\left( {100\pi t + \dfrac{\pi }{3}} \right)V\). Điện áp tức thời ở hai đầu tụ có biểu thức như thế nào:
Cài đặt máy tính ở chế độ radian SHIFT MODE 4
Bấm máy tính MODE 2 (Chọn CMPLX)
Cảm kháng và dung kháng của đoạn mạch \({Z_L} = \omega L = 100\pi .\dfrac{2}{\pi } = 200\Omega \) ; \({Z_C} = \dfrac{1}{{\omega C}} = \dfrac{1}{{100\pi \dfrac{{{{10}^{ - 4}}}}{\pi }}} = 100\Omega \)
Cường độ dòng điện trong mạch \(\overline I = \dfrac{{\overline {{U_L}} }}{{\overline {{Z_L}} }} = \dfrac{{100\sqrt 2 \angle \dfrac{\pi }{3}}}{{200i}}\) SHIFT 2 3 =
Ta đọc kết quả \(\overline I = \dfrac{{\sqrt 2 }}{2}\angle - \dfrac{\pi }{6}\)
Điện áp tức thời hai đầu tụ điện \(\overline {{U_C}} = \overline I .\overline {{Z_C}} = \left( {\dfrac{{\sqrt 2 }}{2}\angle - \dfrac{\pi }{6}} \right).\left( { - 100i} \right)\) SHIFT 2 3 =
Ta đọc kết quả \({U_C} = 50\sqrt 2 \angle - \dfrac{{2\pi }}{3}\)
Vậy biểu thức điện áp hai đầu tụ điện \({u_C} = 50\sqrt 2 \cos \left( {100\pi t - \dfrac{{2\pi }}{3}} \right)V\)
Đặt điện áp xoay chiều vào hai đầu đoạn mạch có điện trở R, cuộn cảm thuần L và tụ điện C mắc nối tiếp. Biết \(R = 10\Omega ,L = \displaystyle{{0,1} \over \pi }H,C = \displaystyle{{{{10}^{ - 3}}} \over {2\pi }}F\) và điện áp giữa hai đầu cuộn cảm là \({u_L} = 20\sqrt 2 \cos \left( {100\pi t + \displaystyle{\pi \over 2}} \right)V\). Biểu thức điện áp tức thời giữa hai đầu đoạn mạch là:
Cài đặt máy tính ở chế độ radian SHIFT MODE 4
Bấm máy tính MODE 2 (Chọn CMPLX)
Cảm kháng của cuộn dây ZL = ωL = 10 Ω
Dung kháng của tụ điện ZC = 1/ωC = 20 Ω
Tổng trở của đoạn mạch là \(\overline Z = R + \left( {{Z_L} - {Z_C}} \right)i = 10 - 10i\)
Cường độ dòng điện trong mạch là \(\overline I = \displaystyle{{\overline {{U_L}} } \over {\overline {{Z_L}} }} = {{20\sqrt 2 \angle {\pi \over 2}} \over {10i}}\) SHIFT 2 3 =
Ta đọc kết quả \(\overline I = 2\sqrt 2 \angle 0\)
Điện áp hiệu dụng hai đầu đoạn mạch \(\overline U = \overline I .\overline Z = \left( {2\sqrt 2 \angle 0} \right)\left( {10 - 10i} \right)\) SHIFT 2 3 =
Ta đọc kết quả \(\overline U = 40\angle - \displaystyle{\pi \over 4}\)
Biểu thức điện áp hai đầu đoạn mạch là \(u = 40cos(100πt – π/4) V\)
Một đoạn mạch điện gồm một cuộn dây thuần cảm có độ tự cảm \(L = 1/π (H)\) và điện trở thuần \(R = 100 Ω\). Đặt vào hai đầu mạch một điện áp xoay chiều \(u = 200cos(100πt + π/4) V\) thì biểu thức nào sau đây là của điện áp hai đầu cuộn cảm thuần ?
Cài đặt máy tính ở chế độ radian SHIFT MODE 4
Bấm máy tính MODE 2 (Chọn CMPLX)
Cảm kháng của cuộn dây ZL = ωL = 100 Ω
Tổng trở của đoạn mạch \(\overline Z = R + {Z_L}i = 100 + 100i\)
Cường độ dòng điện trong mạch \(\overline I = \displaystyle{{\overline U } \over {\overline Z }} = {{200\angle \displaystyle{\pi \over 4}} \over {100 + 100i}}\) SHIFT 2 3 =
Ta đọc kết quả \(\overline I = \sqrt 2 \angle 0\)
Điện áp hiệu dụng hai đầu cuộn cảm là \(\overline {{U_L}} = \overline I .\overline {{Z_L}} = \left( {\sqrt 2 \angle 0} \right).100i\) SHIFT 2 3 =
Ta đọc kết quả \(\overline {{U_L}} = 100\sqrt 2 \angle \displaystyle{\pi \over 2}\)
Vậy biểu thức điện áp hai đầu cuộn cảm là \(u_L=100\sqrt 2 \cos \left( {100\pi t + \displaystyle{\pi \over 2}} \right)V\)
Đoạn mạch AC có điện trở thuần, cuộn dây thuần cảm và tụ điện mắc nối tiếp. B là một điểm trên AC với \({u_{AB}}\; = cos100\pi t{\rm{ }}\left( V \right)\) và \({u_{BC}} = \sqrt 3 cos\left( {100\pi t - \displaystyle{\pi \over 2}} \right)(V)\). Tìm biểu thức hiệu điện thế \(u_{AC}\):
Cài đặt máy tính ở chế độ radian SHIFT MODE 4
Bấm máy tính MODE 2 (Chọn CMPLX)
Ta có uAC = uAB + uBC
\(\overline {{U_{AC}}} = 1\angle 0 + \sqrt 3 \angle - \displaystyle{\pi \over 2}\) SHIFT 2 3 =
Ta đọc kết quả \(\overline {{U_{AC}}} = 2\angle - \displaystyle{\pi \over 3}\)
Biểu thức điện áp uAC là \({u_{AC}}\, = \,2{\rm{cos}}\left( {100\pi t\, - \,\displaystyle{\pi \over 3}} \right)V\)
Cho mạch điện không phân nhánh RLC: \(R = 80 Ω\) , cuộn dây có điện trở \(20 Ω\), có độ tự cảm \(L=0,636H\), tụ điện có điện dung \(C=31,8μF\). Hiệu điện thế hai đầu mạch là \(u = 200cos(100πt-\dfrac{\pi }{4}\)) (V) thì biểu thức cường độ dòng điện chạy qua mạch điện là:

Dòng điện chạy qua một đoạn mạch gồm cuộn dây thuần cảm có L = 1/10π (H), mắc nối tiếp với một tụ điện C = 2.10-4/π (F) có biểu thức \(i = 2\sqrt 2 \cos (100\pi t - \pi /6)\) (A). Biểu thức điện áp hai đầu mạch có thể là:

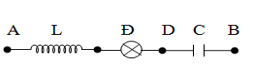
Mạch như hình vẽ.
Biết Đ: 100V – 100W ; L =\(\dfrac{1}{\pi }\)H , C = \(\dfrac{{50}}{\pi }\mu F\), uAD = 200\(\sqrt 2 \)sin 100πt+\(\dfrac{\pi }{6}\) )(V).
Biểu thức uAB có dạng:

Mạch như hình vẽ
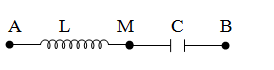
${u_{AB}} = 120\sqrt 2 cos\left( {100\pi t} \right)V$. Dùng vôn kế có điện trở rất lớn đo giữa $A$ và $M$ thì thấy nó chỉ $120V$, và $u_{AM}$ nhanh pha hơn $u_{AB}$ \(\dfrac{\pi }{2}\) . Biểu thức $u_{MB}$ có dạng:

Cho mạch điện xoay chiều gồm có R = 40Ω, cuộn dây thuần cảm có L = 1/2π(H) và tụ điện C. Điện áp hai đầu mạch u = 160cos100πt(V). Biết biểu thức cường độ dòng điện trong mạch là \(i = 2\sqrt 2 \cos (100\pi t + \pi /4)\) )(A). Tìm điện dung của tụ điện.
+ Cách 1 : Phương pháp đại số
Cách A: Ta có : R = 40Ω, ZL = 50Ω
\(Z = \frac{{{U_0}}}{{{I_0}}} = \frac{{160}}{{2\sqrt 2 }} = 40\sqrt 2 = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \to \left| {{Z_L} - {Z_C}} \right| = 40 \to \left( \begin{array}{l}{Z_C} = 10\\{Z_C} = 90\end{array} \right.\)
Do I nhanh pha hơn u => ZC > ZL => ZC = 90 => C = 1/9000π (F)
Cách B : Độ lệch pha của u so với i : - π/4
\(\tan - \frac{\pi }{4} = \frac{{{Z_L} - {Z_C}}}{R} = - 1 \to {Z_C} = 90\Omega \to C = \frac{1}{{9000\pi }}F\)
+ Cách 2 : Phương pháp casio giải điện xoay chiều

Cho đoạn mạch xoay chiều như hình vẽ
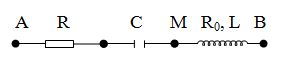
$R{\rm{ }} = {\rm{ }}50\Omega ,{\rm{ }}C = \dfrac{{{{2.10}^{ - 4}}}}{\pi }\left( F \right)$ , ${u_{AM}} = {\rm{ }}80cos100\pi t\left( V \right)$ , ${u_{MB}} = 200\sqrt 2 cos(100\pi t + \dfrac{\pi }{2})\left( V \right)$ . Giá trị của $R_0$ và $L$ là:

Đoạn mạch AC có điện trở thuần, cuộn dây thuần cảm và tụ điện mắc nối tiếp. B là một điểm trên AC với \({u_{AB}} = \sin 100\pi t\left( V \right)\); \({u_{BC}} = \sqrt 3 \sin \left( {100\pi t - \dfrac{\pi }{2}} \right)\left( V \right)\) . Tính biểu thức hiệu điện thế uAC.
Chuyển uAB và uBC sang dạng số phức
\(\begin{array}{l}\left\{ {\begin{array}{*{20}{l}}{{u_{AB}} = {\rm{ }}1}\\{{u_{BC}} = \sqrt 3 \angle - \dfrac{\pi }{2}}\end{array}} \right. \\\to {u_{AC}} = {u_{AB}} + {u_{BC}} = 1 + \sqrt 3 \angle - \dfrac{\pi }{2} = 2\angle - \dfrac{\pi }{3}\\ \to {u_{AC}} = 2\sin \left( {100\pi t - \dfrac{\pi }{3}} \right)\end{array}\)
Mạch điện nối tiếp R, L, C trong đó cuộn dây thuần cảm (ZL < ZC). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều \(u = 200\sqrt 2 {\rm{cos}}\left( {100\pi t + \dfrac{\pi }{4}} \right)V\). Khi \(R = 50Ω\) công suất mạch đạt giá trị cực đại. Biểu thức dòng điện qua mạch lúc đó:
Ta có, khi R = 50Ω công suất mạch đạt giá trị cực đại
\( \to \left| {{Z_L} - {Z_C}} \right| = R = 50\Omega \)
Do ZL < ZC => ZL - ZC = -50
\(\begin{array}{l}i = \dfrac{u}{Z} = \dfrac{{200\sqrt 2 \angle \dfrac{\pi }{4}}}{{50 - 50i}} = 4\angle \dfrac{\pi }{2}\\ \to i = 4c{\rm{os}}\left( {100\pi t + \dfrac{\pi }{2}} \right)A\end{array}\)
Cho mạch điện như hình vẽ. \(R = 50\,(\Omega ),\,\,L = \frac{1}{\pi }(H)\). Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều \(u = 220\sqrt 2 \sin \left( {100\pi t} \right)\,\,(V)\). Biết tụ điện có điện dung C thay đổi được. Tính C để hiệu điện thế cùng pha cường độ dòng điện.
+ Cách 1:
Ta có: hiệu điện thế cùng pha với cường độ dòng điện => Mạch cộng hưởng dao động
=> ZL = ZC = 100Ω
=> C = 1/1000π F
+ Cách 2:
Biểu diễn các đại lượng dưới dạng số phức:
\({u_{AB}} = 220\sqrt 2 \,\)
\({Z_L} = L\omega = \frac{1}{\pi } \cdot 100\pi = 100\,\,(\Omega )\)
\(Z_{AB}^{} = R + \left( {{Z_L} - {Z_C}} \right)i = 50 + \left( {100 - {Z_C}} \right)i\)
Ta có:
\({i_{AB}} = \frac{{{u_{AB}}}}{{Z_{AB}^{}}} = 220\sqrt 2 :\left( {50 + \left( {100 - {Z_C}} \right)i} \right)\)
Để hiệu điện thế cùng pha với cường độ dòng điện thì i = I0. Khi đó, thành phần ảo trong tổng trở Z phải bằng 0
\( \Rightarrow 100 - {Z_C} = 0 \Rightarrow \,\,{Z_C} = 100\,\,\)mà \(\,{Z_C} = \frac{1}{{C\omega }}\)
\( \Rightarrow C = \frac{1}{{{Z_C}\omega }} = \frac{1}{{100 \cdot 100\pi }} = \frac{{{{10}^{ - 4}}}}{\pi }\,\,(F)\)
Đặt một điện áp xoay chiều vào hai đầu một cuộn dây chỉ có độ tự cảm L = \(\frac{1}{{2\pi }}H\) thì cường độ dòng điện qua cuộn dây có biểu thức : \(i{\rm{ }} = {\rm{ }}3\sqrt 2 {\rm{cos}}\left( {100\pi t + \frac{\pi }{6}} \right)\) (A). Nếu đặt điện áp nói trên vào hai bản tụ của tụ điện có điện dung \(C{\rm{ }} = \frac{1}{\pi }{.10^{ - 4}}\)F thì biểu thức nào trong các biểu thức sau đúng với biểu thức dòng điện ?
\(\begin{array}{l}u = {i_1}{Z_L}\\ \to {i_2} = \frac{u}{{{Z_C}}} = \frac{{{i_1}{Z_L}}}{{{Z_C}}} = 3\sqrt 2 \angle \frac{\pi }{6}x\left( {50i} \right):\left( { - 100i} \right) = 1,5\sqrt 2 \angle - \frac{{5\pi }}{6}\\ \to {i_2} = 1,5\sqrt 2 {\rm{cos}}\left( {100\pi t - \frac{{5\pi }}{6}} \right)\end{array}\)
Một đoạn mạch gồm một tụ điện có dung kháng ZC = 100Ω cuộn dây có cảm kháng ZL=200\(\Omega \) mắc nối tiếp nhau. Điện áp tại hai đầu cuộn cảm có dạng \({{\rm{u}}_{\rm{L}}}{\rm{ = 100cos(100\pi t + }}\dfrac{{\rm{\pi }}}{{\rm{6}}}{\rm{)V}}\). Biểu thức điện áp ở hai đầu tụ điện có dạng là:
\({u_C} = i{Z_C} = \dfrac{{{u_L}}}{{{Z_L}}}{Z_C} \\= 100\angle \dfrac{\pi }{6}:(200i)x( - 100i) \\= 50\angle - \dfrac{{5\pi }}{6}\)
=> Biểu thức giữa hai đầu tụ điện: \(u_C=50cos(100\pi t - \dfrac{5\pi}{6})V\)
Nếu đặt vào hai đầu một mạch điện chứa một điện trở thuần và một cuộn cảm thuần mắc nối tiếp mộ điện áp xoay chiều có biểu thức \(u = 100\sqrt 2 c{\rm{os}}\left( {\omega t + \frac{{7\pi }}{{12}}} \right)V\) thì khi đó điện áp hai đầu điện trở thuần có biểu thức \({u_R} = 100c{\rm{os}}\left( {\omega t + \frac{\pi }{3}} \right)V\) . Biểu thức điện áp giữa hai đầu cuộn cảm thuần sẽ là:
Ta có:
\(\begin{array}{l}u = {u_R} + {u_L} \to {u_L} = u - {u_R} = 100\sqrt 2 \angle \frac{{7\pi }}{{12}} - 100\angle \frac{\pi }{3} = 100\angle \frac{{5\pi }}{6}\\ \to {u_L} = 100c{\rm{os}}\left( {\omega t + \frac{{5\pi }}{6}} \right)V\end{array}\)
Cho đoạn mạch xoay chiều không phân nhánh gồm điện trở thuần R, cuộn dây thuần cảm L; tụ điện có điện dung C. Đặt vào 2 đầu đoạn mạch một điện áp xoay chiều thì điện áp tức thời giữa hai đầu điện trở là: \({u_R} = 100c{\rm{os}}\left( {100\pi t + \frac{\pi }{4}} \right)V\), giữa hai đầu cuộn cảm thuần là: \({u_L} = 120c{\rm{os}}\left( {100\pi t + \frac{{3\pi }}{4}} \right)V\), giữa hai đầu tụ điện là \({u_C} = 20c{\rm{os}}\left( {100\pi t - \frac{\pi }{4}} \right)V\). Biểu thức giữa hai đầu đoạn mạch là:
Ta có:
\(\begin{array}{l}u = {u_R} + {u_L} + {u_C} \to u = 100\angle \frac{\pi }{4} + 120\angle \frac{{3\pi }}{4} + 20\angle - \frac{\pi }{4} = 100\sqrt 2 \angle \frac{\pi }{2}\\ \to u = 100\sqrt 2 c{\rm{os}}\left( {\omega t + \frac{\pi }{2}} \right)V\end{array}\)
Đặt điện áp xoay chiều \({u_{AB}} = 100\sqrt 2 {\rm{cos}}\left( {100\pi t} \right)V\) vào mạch RLC nối tiếp theo thứ tự là điện trở R, cuộn dây thuần cảm có L thay đổi được và \(C\). Khi \(L =L_1= 1/π H\) hay \(L =3L_1\) thì mạch có cùng công suất nhưng dòng điện i1 và i2 lệch pha nhau \(\dfrac{2\pi}{3}\). Biểu thức của hiệu điện thế uMB (M là điểm nằm giữa cuộn dây và tụ điện) khi L = L1 là:
Cảm kháng:
\({Z_{{L_1}}} = \omega {L_1} = 100\Omega \)
Mạch có L thay đổi mà có cùng công suất P thì:
\(\left\{ \begin{array}{l}{Z_C} = \dfrac{{{Z_{{L_1}}} + {Z_{{L_2}}}}}{2} = 2{Z_{{L_1}}} = 200\Omega \\{\varphi _{{i_1}/{i_2}}} = 2\alpha = \dfrac{{2\pi }}{3}\end{array} \right. \\\to {\varphi _1} = \dfrac{\pi }{3} \\\to R = \dfrac{{{Z_{{L_1}}}}}{{\sqrt 3 }} = \dfrac{{100}}{{\sqrt 3 }}\Omega \)
Điện áp:
\(\begin{array}{l}{u_{MB}} = i.{Z_{MB}} = \dfrac{u}{Z}{Z_{MB}} = 100\sqrt 2 \div \left( {\dfrac{{100}}{{\sqrt 3 }} + \left( {100 - 200} \right)i} \right)x( - 200i)\\ = 244,9489743\angle - \dfrac{\pi }{6}\end{array}\)

