Phản ứng hạt nhân - Bài tập xác định động năng, vận tốc, góc của các hạt

Ta có:

+ Năng lượng của phản ứng:

 \(\begin{array}{l}\Delta E = \left( {{m_t} - {m_s}} \right){c^2}\\ = \left( {\left( {{m_p} + {m_{Be}}} \right) - \left( {{m_{Li}} + {m_X}} \right)} \right){c^2}\\ = \left( {\left( {1,0073u + 9,01219u} \right) - \left( {6,01513u + 4,0015u} \right)} \right){c^2}\\ = 2,{86.10^{ - 3}}u{c^2}\\ = 2,66266MeV\end{array}\)

+ Lại có:

\(\begin{array}{l}{{\rm{W}}_{{d_p}}} + \Delta E = {{\rm{W}}_{{d_{Li}}}} + {{\rm{W}}_{{d_X}}}\\ \Rightarrow {{\rm{W}}_{{d_X}}} = {{\rm{W}}_{{d_p}}} + \Delta E - {W_{{d_{Li}}}}\\ = 5,45 + 2,66266 - 3,05\\ = 5,06266MeV\end{array}\)

+ Phản ứng thu năng lượng \(\Delta E =  - 1,21MeV\)

+ Áp dụng định luật bảo toàn năng lượng và dữ kiện đầu bài, ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}{{\rm{W}}_{{d_O}}}{\rm{ + }}{W_{{d_p}}} = \Delta E + {{\rm{W}}_{{d_\alpha }}} =  - 1,21 + 4,21 = 3(MeV)\\{{\rm{W}}_{{d_O}}} = 2{W_{{d_p}}}\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}{{\rm{W}}_{{d_O}}} = \left( {{{\rm{W}}_{{d_\alpha }}} + \Delta E} \right)\dfrac{2}{{2 + 1}} = 2(MeV)\\{W_{{d_n}}} = \left( {{{\rm{W}}_{{d_\alpha }}} + \Delta E} \right)\dfrac{1}{{2 + 1}} = 1(MeV)\end{array} \right.\end{array}\)

Gọi hạt nhân tạo thành sau phản ứng là X

Ta có:

\(\begin{array}{l}{\rm{2}}{W_{{d_X}}} = \Delta E + {{\rm{W}}_{{d_\alpha }}} = 13,8 + 1,8 = 15,6(MeV)\\ \to {W_{{d_X}}} = \dfrac{{15,6}}{2} = 7,8(MeV)\end{array}\)

\({v_{{X_1}}} = {\rm{ }}2{v_{{X_2}}} \to {{\rm{W}}_{{d_{{X_1}}}}} = 4{{\rm{W}}_{{d_{{X_2}}}}}\)

\(\begin{array}{l}\left\{ \begin{array}{l}{{\rm{W}}_{{d_{{X_1}}}}}{\rm{ + }}{{\rm{W}}_{{d_{{X_2}}}}} = \Delta E + {{\rm{W}}_{{d_p}}} = 17,4 + 1,2 = 18,6(MeV)\\{{\rm{W}}_{{d_{{X_1}}}}} = 4{{\rm{W}}_{{d_{{X_2}}}}}\end{array} \right.\\ \to \left\{ \begin{array}{l}{{\rm{W}}_{{d_{X2}}}} = \left( {{{\rm{W}}_{{d_p}}} + \Delta E} \right)\dfrac{4}{{4 + 1}} = 18,6.\dfrac{4}{5} = 14,88(MeV)\\{{\rm{W}}_{{d_{X1}}}} = \left( {{{\rm{W}}_{{d_p}}} + \Delta E} \right)\dfrac{1}{{4 + 1}} = 18,6.\dfrac{1}{5} = 3,72(MeV)\end{array} \right.\end{array}\)

\(A{\rm{ }} + {\rm{ }}B \to C{\rm{ }} + {\rm{ }}D\)

\({v_C} = {v_D} \to \dfrac{{{{\rm{W}}_C}}}{{{{\rm{W}}_D}}} = \dfrac{{{m_C}{v_C}^2}}{{{m_D}{v_D}^2}} = \dfrac{{{m_C}}}{{{m_D}}}\)    (1)

Mặt khác: \({{\rm{W}}_C} + {{\rm{W}}_D} = {{\rm{W}}_A} + \Delta E\)    (2)

Từ (1) ta suy ra: \({{\rm{W}}_C} = \dfrac{{{m_C}}}{{{m_D}}}{{\rm{W}}_D}\)  thế vào (2) ta được:

\(\begin{array}{l}\dfrac{{{m_C}}}{{{m_D}}}{{\rm{W}}_D} + {{\rm{W}}_D} = {{\rm{W}}_A} + \Delta E\\ \Leftrightarrow \left( {\dfrac{{{m_C}}}{{{m_D}}} + 1} \right){{\rm{W}}_D} = {{\rm{W}}_A} + \Delta E\\ \Leftrightarrow \left( {\dfrac{{{m_C} + {m_D}}}{{{m_D}}}} \right){{\rm{W}}_D} = {{\rm{W}}_A} + \Delta E\\ \Rightarrow {W_D} = \left( {{{\rm{W}}_A} + \Delta E} \right)\dfrac{{{m_D}}}{{{m_C} + {m_D}}}\end{array}\)

\(_7^{14}N + \alpha  \to _8^{17}O + _1^1p\)

Ta có: \(\overrightarrow {{v_O}}  = \overrightarrow {{v_p}} \)

+ Áp dụng định luật bảo toàn động lượng: \(\overrightarrow {{P_t}}  = \overrightarrow {{P_s}}  \leftrightarrow {m_\alpha }\overrightarrow {{v_\alpha }}  = {m_O}\overrightarrow {{v_O}}  + {m_p}\overrightarrow {{v_p}} \)

\(\begin{array}{l}\overrightarrow {{v_O}}  = \overrightarrow {{v_p}}  \to {m_\alpha }\overrightarrow {{v_\alpha }}  = \left( {{m_O} + {m_p}} \right)\overrightarrow {{v_O}} \\ \to \overrightarrow {{v_O}}  = \overrightarrow {{v_p}}  = \dfrac{{{m_\alpha }\overrightarrow {{v_\alpha }} }}{{{m_O} + {m_p}}} = \dfrac{4}{{17 + 1}}\overrightarrow {{v_\alpha }}  = \dfrac{2}{9}\overrightarrow {{v_\alpha }} \end{array}\)

+ Ta có: \(\left\{ \begin{array}{l}{{\rm{W}}_O} = \dfrac{1}{2}{m_O}v_O^2\\{{\rm{W}}_\alpha } = \dfrac{1}{2}{m_\alpha }v_\alpha ^2\end{array} \right.\)

\( \Rightarrow \dfrac{{{{\rm{W}}_O}}}{{{{\rm{W}}_\alpha }}} = \dfrac{{{m_O}v_O^2}}{{{m_\alpha }v_\alpha ^2}} = \dfrac{{17.{{\left( {\dfrac{2}{9}{v_\alpha }} \right)}^2}}}{{4.v_\alpha ^2}} = \dfrac{{17}}{{81}}\)

Ta có phương trình: \({}_2^4He + {}_7^{14}N \to {}_1^1p + {}_8^{17}X\)

k_p + k_x – k_He = 4E = -1,21 (thu năng lượng)

Ta suy ra: 0,5m_p(v_x.8,5)² + 0,5m_xv_x² – 4,01 = -1,21

=> v_x = 2,46.10⁶m/s

\(_7^{14}N + \alpha  \to _8^{17}O + _1^1p\)

Ta có: \(\overrightarrow {{v_O}}  = \overrightarrow {{v_p}} \)

Áp dụng định luật bảo toàn động lượng: \(\overrightarrow {{P_t}}  = \overrightarrow {{P_s}}  \leftrightarrow {m_\alpha }\overrightarrow {{v_\alpha }}  = {m_O}\overrightarrow {{v_O}}  + {m_p}\overrightarrow {{v_p}} \)

\(\begin{array}{l}\overrightarrow {{v_O}}  = \overrightarrow {{v_p}}  \to {m_\alpha }\overrightarrow {{v_\alpha }}  = \left( {{m_O} + {m_p}} \right)\overrightarrow {{v_O}} \\ \to \overrightarrow {{v_O}}  = \overrightarrow {{v_p}}  = \dfrac{{{m_\alpha }\overrightarrow {{v_\alpha }} }}{{{m_O} + {m_p}}}\end{array}\)

\(\left\{ \begin{array}{l}{{\rm{W}}_O} = \dfrac{1}{2}{m_O}v_O^2\\{{\rm{W}}_p} = \dfrac{1}{2}{m_p}v_p^2\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_O} = \dfrac{{{m_O}{m_\alpha }}}{{{{\left( {{m_O} + {m_p}} \right)}^2}}}{{\rm{W}}_\alpha }\\{{\rm{W}}_p} = \dfrac{{{m_p}{m_\alpha }}}{{{{\left( {{m_O} + {m_p}} \right)}^2}}}{{\rm{W}}_\alpha }\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_O} = 0,21{{\rm{W}}_\alpha }\\{{\rm{W}}_p} = 0,012{W_\alpha }\end{array} \right.\)

Mặt khác,

\(\begin{array}{l}\Delta E + {{\rm{W}}_\alpha } = {{\rm{W}}_O} + {{\rm{W}}_p}\\ \to \Delta E = {{\rm{W}}_O} + {{\rm{W}}_p} - {{\rm{W}}_\alpha } \leftrightarrow  - 1,21 = 0,21{{\rm{W}}_\alpha } + 0,012{{\rm{W}}_\alpha } - {{\rm{W}}_\alpha }\\ \to {{\rm{W}}_\alpha } = 1,555(MeV)\end{array}\)

=> Động năng của hạt Oxi là: \({{\rm{W}}_O} = 0,21{W_\alpha } = 0,21.1,555 \approx 0,33MeV\)

\(_7^{14}N + \alpha  \to _8^{17}O + _1^1p\)

Ta có: \(\overrightarrow {{v_O}}  = \overrightarrow {{v_p}} \)

Áp dụng định luật bảo toàn động lượng: \(\overrightarrow {{P_t}}  = \overrightarrow {{P_s}}  \leftrightarrow {m_\alpha }\overrightarrow {{v_\alpha }}  = {m_O}\overrightarrow {{v_O}}  + {m_p}\overrightarrow {{v_p}} \)

\(\begin{array}{l}\overrightarrow {{v_O}}  = \overrightarrow {{v_p}}  \to {m_\alpha }\overrightarrow {{v_\alpha }}  = \left( {{m_O} + {m_p}} \right)\overrightarrow {{v_O}} \\ \to \overrightarrow {{v_O}}  = \overrightarrow {{v_p}}  = \dfrac{{{m_\alpha }\overrightarrow {{v_\alpha }} }}{{{m_O} + {m_p}}}\end{array}\)

\(\left\{ \begin{array}{l}{{\rm{W}}_O} = \dfrac{1}{2}{m_O}v_O^2\\{{\rm{W}}_p} = \dfrac{1}{2}{m_p}v_p^2\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_O} = \dfrac{{{m_O}{m_\alpha }}}{{{{\left( {{m_O} + {m_p}} \right)}^2}}}{{\rm{W}}_\alpha }\\{{\rm{W}}_p} = \dfrac{{{m_p}{m_\alpha }}}{{{{\left( {{m_O} + {m_p}} \right)}^2}}}{{\rm{W}}_\alpha }\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_O} = 0,21{{\rm{W}}_\alpha }\\{{\rm{W}}_p} = 0,012{W_\alpha }\end{array} \right.\)

Mặt khác,

\(\begin{array}{l}\Delta E + {{\rm{W}}_\alpha } = {{\rm{W}}_O} + {{\rm{W}}_p}\\ \to \Delta E = {{\rm{W}}_O} + {{\rm{W}}_p} - {{\rm{W}}_\alpha } \leftrightarrow  - 1,21 = 0,21{{\rm{W}}_\alpha } + 0,012{{\rm{W}}_\alpha } - {{\rm{W}}_\alpha }\\ \to {{\rm{W}}_\alpha } = 1,555(MeV)\end{array}\)

=> Động năng của hạt proton là: \({{\rm{W}}_p} = 0,012{W_\alpha } = 0,012.1,555 \approx 0,019MeV\)

Ta có:

\(\begin{array}{l}\overrightarrow 0  = {m_\alpha }\overrightarrow {{v_\alpha }}  + {m_n}\overrightarrow {{v_n}}  \to {m_\alpha }\overrightarrow {{v_\alpha }}  =  - {m_n}\overrightarrow {{v_n}} \\ \to {\left( {{m_\alpha }\overrightarrow {{v_\alpha }} } \right)^2} = {\left( { - {m_n}\overrightarrow {{v_n}} } \right)^2} \to {m_\alpha }{{\rm{W}}_\alpha } = {m_n}{{\rm{W}}_n}\\ \to {{\rm{W}}_\alpha } = \dfrac{1}{4}{{\rm{W}}_n}\end{array}\)

Mặt khác: \(\Delta E = {{\rm{W}}_\alpha } + {{\rm{W}}_n} = \dfrac{1}{4}{{\rm{W}}_n} + {{\rm{W}}_n} \to {{\rm{W}}_n} = \dfrac{{17,6}}{{1,25}} = 14,08(MeV)\)

=> Động năng của Heli là: \({{\rm{W}}_\alpha } = \dfrac{1}{4}{{\rm{W}}_n} = \dfrac{{14,08}}{4} = 3,52MeV\)

\(\alpha  + _4^9Be \to X + n\)

Ta có: \(\widehat {\overrightarrow {{v_X}} ,\overrightarrow {{v_n}} } = {90^0}\)

\(\begin{array}{l}\overrightarrow {{v_X}}  \bot \overrightarrow {{v_n}}  \to \left\{ \begin{array}{l}P_\alpha ^2 = P_X^2 + P_n^2\\{{\rm{W}}_{{d_\alpha }}} + \Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_n}}}\end{array} \right. \to \left\{ \begin{array}{l}{m_\alpha }{{\rm{W}}_{{d_\alpha }}} = {m_X}{{\rm{W}}_{{d_X}}} + {m_n}{{\rm{W}}_{{d_n}}}\\{{\rm{W}}_{{d_\alpha }}} + \Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_n}}}\end{array} \right.\\ \to \left\{ \begin{array}{l}3,968{m_n}.5,3 = 11,8965{m_n}{{\rm{W}}_{{d_X}}} + {m_n}{{\rm{W}}_{{d_n}}}\\5,3 + 5,6791 = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_n}}}\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_X} = 0,922(MeV)\\{{\rm{W}}_n} = 10,06(MeV)\end{array} \right.\end{array}\)

\(_1^1p + _4^9Be \to _2^4\alpha  + _3^6X\)

Ta có: \(\widehat {\overrightarrow {{v_\alpha }} ,\overrightarrow {{v_p}} } = {90^0}\)

\(\begin{array}{l}\overrightarrow {{v_\alpha }}  \bot \overrightarrow {{v_p}}  \to \left\{ \begin{array}{l}P_X^2 = P_\alpha ^2 + P_p^2\\{{\rm{W}}_{{d_p}}} + \Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_\alpha }}}\end{array} \right. \to \left\{ \begin{array}{l}{m_X}{{\rm{W}}_{{d_X}}} = {m_\alpha }{{\rm{W}}_{{d_\alpha }}} + {m_p}{{\rm{W}}_{{d_p}}}\\{{\rm{W}}_{{d_p}}} + \Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_\alpha }}}\end{array} \right.\\ \to \left\{ \begin{array}{l}6.{{\rm{W}}_{{d_X}}} = 4.4 + 1.5,45\\\Delta E = {{\rm{W}}_{{d_X}}} + {{\rm{W}}_{{d_\alpha }}} - {{\rm{W}}_{{d_p}}}\end{array} \right. \to \left\{ \begin{array}{l}{{\rm{W}}_X} = 3,575(MeV)\\\Delta E = 3,575 + 4 - 5,45 = 2,125(MeV)\end{array} \right.\end{array}\)

\(_1^1p + _{11}^{23}Na \to _2^4\alpha  + _{10}^{20}X\)

Gọi \(\varphi  = \widehat {\overrightarrow {{v_\alpha }} ;\overrightarrow {{v_p}} }\)

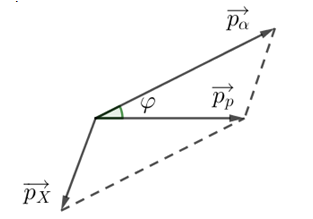
Ta có:

\(\begin{array}{l}p_X^2 = p_p^2 + p_\alpha ^2 + 2{p_p}{p_\alpha }cos\varphi \\ \Leftrightarrow {m_X}{{\rm{W}}_X} = {m_p}{{\rm{W}}_p} + {m_\alpha }{{\rm{W}}_\alpha } - 2cos\varphi \sqrt {{m_p}{{\rm{W}}_p}{m_\alpha }{{\rm{W}}_\alpha }} \\ \Leftrightarrow 20.2,648 = 1.5,58 + 4.6,6 - 2cos\varphi \sqrt {1.5,58.4.6,6} \\ \Rightarrow cos\varphi  =  - 0,86428\\ \Rightarrow \varphi  \approx {150^0}\end{array}\)

Ta có hạt proton chuyển động theo hướng hợp với hướng chuyển động của hạt \(\alpha \) một góc \({60^0}\), vẽ giản đồ ta được:

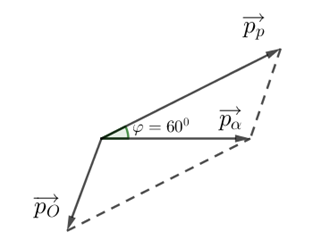
Ta suy ra:

\(\begin{array}{l}p_O^2 = p_\alpha ^2 + p_p^2 - 2{p_\alpha }{p_p}cos\varphi \\ \Leftrightarrow {m_O}{{\rm{W}}_O} = {m_\alpha }{{\rm{W}}_\alpha } + {m_p}{{\rm{W}}_p} - 2cos\varphi \sqrt {{m_\alpha }{{\rm{W}}_\alpha }{m_p}{{\rm{W}}_p}} \\ \Leftrightarrow 17.{{\rm{W}}_O} = 4.4 + 1.2,09 - 2cos{60^0}\sqrt {4.4.1.2,09} \\ \Rightarrow {{\rm{W}}_O} = 0,724MeV\end{array}\)

Lại có: Năng lượng \(\Delta E = {{\rm{W}}_s} - {{\rm{W}}_t} = \left( {{{\rm{W}}_O} + {{\rm{W}}_P}} \right) - {{\rm{W}}_\alpha } = 0,724 + 2,09 - 4 \approx  - 1,2MeV\)

=> Phản ứng thu năng lượng 1,2MeV

Phương trình: \(p + _3^7Li \to _2^4X + _2^4X\)

Ta có:

\(\begin{array}{l}{{\rm{W}}_{{d_p}}} + \Delta E = 2{{\rm{W}}_{{d_X}}}\\ \Rightarrow {{\rm{W}}_{{d_p}}} = 2{{\rm{W}}_{{d_X}}} - \Delta E = 2{\rm{W}} - \left( { - \dfrac{2}{3}{\rm{W}}} \right){\rm{ = }}\dfrac{8}{3}{\rm{W}}\end{array}\)

Mặt khác: \(\widehat {\overrightarrow {{v_X}} ,\overrightarrow {{v_X}} } = \varphi \)

\(\begin{array}{l}P_p^2 = P_X^2 + P_X^2 + 2{P_X}{P_X}{\rm{cos}}\varphi \\ \Leftrightarrow {m_p}{{\rm{W}}_{{d_p}}} = 2{m_X}{{\rm{W}}_{{d_X}}} + 2{m_X}{{\rm{W}}_{{d_X}}}{\rm{cos}}\varphi \\ \Leftrightarrow \dfrac{8}{3}{\rm{W}} = 2.4{\rm{W}}(1 + c{\rm{os}}\varphi {\rm{)}}\\ \Rightarrow c{\rm{os}}\varphi  =  - \dfrac{2}{3}\end{array}\)

+ Áp dụng định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_p}}  = \overrightarrow {{p_X}}  + \overrightarrow {{p_X}} \) (1)

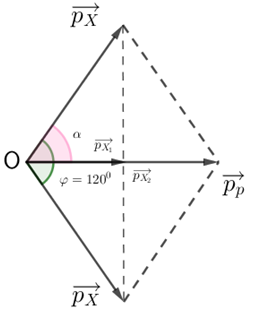
Do \(\left\{ \begin{array}{l}\left( {\widehat {\overrightarrow {{p_X}} ,\overrightarrow {{p_X}} }} \right) = {120^0}\\{v_X} = {v_X}\end{array} \right. \Rightarrow \alpha  = \dfrac{{{{120}^0}}}{2} = {60^0}\)

Chiếu (1) lên phương của \(\overrightarrow {{p_p}} \) ta được:

\({p_p} = {p_{{X_1}}} + {p_{{X_2}}}\)

Lại có: \({p_{{X_1}}} = {p_{{X_2}}} = {p_X}.cos\alpha \)

\(\begin{array}{l} \Rightarrow {p_p} = 2{p_X}cos\alpha \\ \Leftrightarrow {m_p}{v_p} = 2{m_X}{v_X}cos{60^0}\\ \Rightarrow {v_X} = \dfrac{{{m_p}{v_p}}}{{2{m_X}cos{{60}^0}}} = \dfrac{{{m_p}{v_p}}}{{{m_X}}}\end{array}\)

Cách khác: Xét \(\Delta O{p_X}{p_p}\) là tam giác cân có một góc bằng \({60^0}\)

=> Tam giác đó là tam giác đều

\(\begin{array}{l} \Rightarrow {p_X} = {p_p}\\ \Leftrightarrow {m_X}{v_X} = {m_p}{v_p}\\ \Rightarrow {v_X} = \dfrac{{{m_p}{v_p}}}{{{m_X}}}\end{array}\)

+ Phương trình phản ứng:

\(_1^1p + _3^7Li \to _2^4X + _2^4X\)

+ Áp dụng định luật bảo toàn động lượng ta có:

\(\overrightarrow {{p_p}}  = \overrightarrow {{p_X}}  + \overrightarrow {{p_X}} \)

+ Vẽ trên giản đồ, ta được:

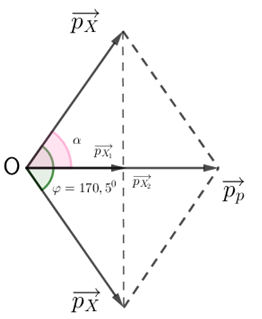
Từ giản đồ ta có:

\(\alpha  = \dfrac{{170,{5^0}}}{2} = 85,{25^0}\)

\({p_{{X_1}}} = {p_{{X_2}}} = {p_X}cos\alpha \)

Chiếu (1) theo phương \(\overrightarrow {{v_p}} \), ta được:

\(\begin{array}{l}{p_p} = {p_{{X_1}}} + {p_{{X_2}}} = 2{p_X}cos\alpha \\ \Leftrightarrow {m_p}{v_p} = 2{m_X}{v_X}cos\alpha \\ \Leftrightarrow {\left( {{m_p}{v_p}} \right)^2} = {\left( {2{m_X}{v_X}cos\alpha } \right)^2}\\ \Leftrightarrow 2{m_p}{{\rm{W}}_p} = 4.2{m_X}{{\rm{W}}_X}co{s^2}\alpha \\ \Rightarrow {{\rm{W}}_X} = \dfrac{{{m_p}{{\rm{W}}_p}}}{{4{m_X}co{s^2}\alpha }} = \dfrac{{1.1}}{{4.4.co{s^2}85,{{25}^0}}} = 9,1145MeV\end{array}\)

+ Năng lượng của phản ứng: \(\Delta E = {{\rm{W}}_s} - {{\rm{W}}_t} = 2{W_X} - {{\rm{W}}_p} = 2.9,1145 - 1 \approx 17,23MeV\)

=> Phản ứng tỏa năng lượng 17,2MeV

Ta có  \({K_X} + {K_H} = 5 - 1,21 = 3,79 \to {K_H} = 3,79 - {K_X}\);

Vẽ giản đồ véc tơ \(\overrightarrow {{P_\alpha }}  = \overrightarrow {{P_X}}  + \overrightarrow {{P_H}} \); gọi \(\beta\) là góc hợp bởi hướng lệch của hạt X so với hướng chuyển động của hạt \(\alpha\) ta có:

\(\cos \beta  = \dfrac{{p_X^2 + p_\alpha ^2 - p_H^2}}{{2{p_X}{p_\alpha }}} = \dfrac{{17{K_X} + 20 - 3,79 + {K_X}}}{{4\sqrt {85} \sqrt {{K_X}} }} = \dfrac{{18\sqrt {{K_X}}  + \dfrac{{16,21}}{{\sqrt {{K_X}} }}}}{{4\sqrt {85} }}\)

Để \(\beta\) đạt giá trị lớn nhất khi K_X = 0,9MeV

Do hạt Li ban đầu đứng yên nên : \(\overrightarrow {{p_p}}  = \overrightarrow {{p_X}}  + \overrightarrow {{p_X}} \)

Mà hai hạt X cùng hợp với phương ban đầu của hạt proton góc 45⁰ nên

\(\begin{array}{l}p_p^2 = 2p_X^2\\ \Rightarrow 2{m_p}{K_p} = 2.2{m_X}{K_X}\\ \Rightarrow m_p^2.v_p^2 = 2m_X^2v_X^2\\ \Rightarrow \dfrac{{{v_X}}}{{{v_p}}} = \dfrac{{{m_p}}}{{\sqrt 2 {m_X}}}\end{array}\)

\( \Rightarrow \dfrac{{v'}}{v} = \dfrac{{{v_X}}}{{{v_p}}} = \dfrac{{{m_p}}}{{\sqrt 2 {m_X}}}\)

Ta có:

\({{\rm{W}}_P} + {{\rm{W}}_n} = \Delta E + {{\rm{W}}_\alpha } =  - 2,7 + {{\rm{W}}_\alpha }\)

\(\dfrac{{{{\rm{W}}_P}}}{{{{\rm{W}}_n}}} = \dfrac{{{m_p}}}{{{m_n}}} = \dfrac{{30}}{1} = 30 \Rightarrow 31{{\rm{W}}_n} =  - 2,7 + {{\rm{W}}_\alpha }\)       (1)

Mặt khác: \({m_\alpha }\overrightarrow {{v_\alpha }}  = {m_P}\overrightarrow {{v_P}}  + {m_n}\overrightarrow {{v_n}}  \Rightarrow {m_\alpha }{v_\alpha } = ({m_P} + {m_n}){v_n} \Leftrightarrow m_\alpha ^2v_\alpha ^2 = {31^2}m_n^2v_n^2\)

\( \Leftrightarrow {m_\alpha }{{\rm{W}}_\alpha } = {31^2}{m_n}{{\rm{W}}_n} \Leftrightarrow {{\rm{W}}_n} = \dfrac{{{m_\alpha }{{\rm{W}}_\alpha }}}{{{{31}^2}{m_n}}} = \dfrac{{4.{{\rm{W}}_\alpha }}}{{{{31}^2}.1}} = \dfrac{{{\rm{4}}{{\rm{W}}_\alpha }}}{{961}}\)  (2)

Từ (1) và (2): \(31\dfrac{{{\rm{4}}{{\rm{W}}_\alpha }}}{{961}} =  - 2,7 + {{\rm{W}}_\alpha } \Rightarrow \dfrac{{{\rm{27}}{{\rm{W}}_\alpha }}}{{31}} = 2,7 \Rightarrow {{\rm{W}}_\alpha } = 3,1(MeV)\)