Câu hỏi:
2 năm trước
Một proton có khối lượng \({m_p}\), có tốc độ \({v_p}\) bắn vào hạt nhân bia đứng yên \(^7Li\). Phản ứng tạo ra 2 hạt X giống hệt nhau có khối lượng \({m_X}\) bay ra với vận tốc có độ lớn bằng nhau và hợp với nhau một góc \({120^0}\). Tốc độ của các hạt X là:
Trả lời bởi giáo viên
Đáp án đúng: c
+ Áp dụng định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_p}} = \overrightarrow {{p_X}} + \overrightarrow {{p_X}} \) (1)
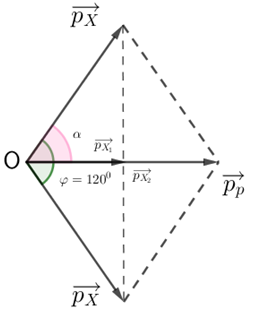
Do \(\left\{ \begin{array}{l}\left( {\widehat {\overrightarrow {{p_X}} ,\overrightarrow {{p_X}} }} \right) = {120^0}\\{v_X} = {v_X}\end{array} \right. \Rightarrow \alpha = \dfrac{{{{120}^0}}}{2} = {60^0}\)
Chiếu (1) lên phương của \(\overrightarrow {{p_p}} \) ta được:
\({p_p} = {p_{{X_1}}} + {p_{{X_2}}}\)
Lại có: \({p_{{X_1}}} = {p_{{X_2}}} = {p_X}.cos\alpha \)
\(\begin{array}{l} \Rightarrow {p_p} = 2{p_X}cos\alpha \\ \Leftrightarrow {m_p}{v_p} = 2{m_X}{v_X}cos{60^0}\\ \Rightarrow {v_X} = \dfrac{{{m_p}{v_p}}}{{2{m_X}cos{{60}^0}}} = \dfrac{{{m_p}{v_p}}}{{{m_X}}}\end{array}\)
Cách khác: Xét \(\Delta O{p_X}{p_p}\) là tam giác cân có một góc bằng \({60^0}\)
=> Tam giác đó là tam giác đều
\(\begin{array}{l} \Rightarrow {p_X} = {p_p}\\ \Leftrightarrow {m_X}{v_X} = {m_p}{v_p}\\ \Rightarrow {v_X} = \dfrac{{{m_p}{v_p}}}{{{m_X}}}\end{array}\)
Hướng dẫn giải:
+ Áp dụng định luật bảo toàn động lượng
+ Vẽ giản đồ véc tơ
+Chọn phương chiếu
Câu hỏi khác
- Bài tập năng lượng liên kết, năng lượng liên kết riêng có lời giải MÔN LÝ lớp 12
- Bài tập tính chất và cấu tạo hạt nhân - bài tập cấu tạo hạt nhân nguyên tử lý 12 có lời giải
- Bài tập phóng xạ - lí thuyết chung lý 12 có lời giải
- Bài tập phản ứng hạt nhân lý 12 có lời giải
- Bài tập phản ứng hạt nhân - bài tập xác định động năng, vận tốc, góc của các hạt lý 12 có lời giải
