Phản ứng hạt nhân

Phương trình phản ứng: \(_5^{10}B + _0^1n \to _Z^AX + _2^4He\)

Áp dụng định luật bảo toàn điện tích và bảo toàn số khối ta có:

\(\left\{ \begin{array}{l}10 + 1 = A + 4\\5 + 0 = Z + 2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}A = 10 + 1 - 4 = 7\\Z = 5 - 2 = 3\end{array} \right.\)

\( \Rightarrow X\) là \(_3^7Li\)

Ta có, các định luật bảo toàn của phản ứng hạt nhân:

+ Bảo toàn điện tích

+ Bảo toàn số nuclon (số khối)

+ Bảo toàn năng lượng

+ Bảo toàn động lượng

Phản ứng hạt nhân không tuân theo định luật bảo toàn số proton

Trong phản hạt nhân, với các đại lượng trên, đại lượng được bảo toàn là điện tích.

Trong phản ứng hạt nhân: Không có định luật bảo toàn số proton.

Ta có:

+ Áp dụng định luật bảo toàn số khối , ta có :

37 + A = 1 + 37 =>  A = 1

+ Áp dụng định luật bảo toàn điện tích, ta có :

17 + Z = 0 + 18 =>  Z = 1

PTPƯ: \({}_0^1n + {}_{92}^{235}U \to {}_{38}^{94}Sr + {}_Z^AX + 2{}_0^1n\)

Áp dụng định luật bảo toàn số khối và định luật bảo toàn điện tích ta có:

+ ĐLBT số khối :

1 + 235 = 94 + A  + 2

=> A = 140

+ ĐLBT điện tích :

0 + 92 = 38 + Z + 0

=> Z = 54

=> Hạt nhân X có : A = 140, Z = 54

=>  Hạt nhân X có cấu tạo gồm : N_p = 54 proton và N_n = 140 – 54 = 86 notron

Ta có phương trình phản ứng là \({}_7^{14}N + {}_2^4He \to {}_Z^AX + {}_1^1p\)

Theo định luật bảo toàn điện tích và định luật bảo toàn số khối ta có:

7 + 2 = 1 + Z

=>  Z = 8

14 + 4 = 1 + A

=> A = 17

Hạt nhân X là \({}_8^{17}O\)

Phương trình phản ứng: \(p + {}_3^7Li \to {}_2^4X + {}_2^4X\)

Ta có, khối lượng của proton \({m_p} = {A_p} = 1u\) , vận tốc của proton \(v = {3.10^7}m/s = 0,1c\)  (\(c = {3.10^8}m/s\) vận tốc ánh sáng)

Động năng của proton \({K_P} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}u.{\left( {0,1c} \right)^2} = \dfrac{1}{2}0,{1^2}.931,5 = 4,6575MeV\)

Theo bảo toàn động lượng: \({\vec p_p} = {\vec p_{X_1}} + {\vec p_{X_2}}\)

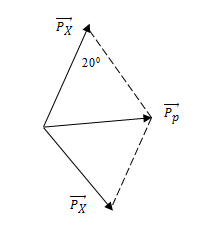
\(P_p^2 = P_X^2 + P_X^2 - 2{P_X}{P_X}c{\rm{os}}{20^0} \Rightarrow {K_p} = {m_X}{K_X} + {m_X}{K_X} - 2{m_X}{K_X}\cos ({20^0}) \Rightarrow {K_X} = 9,653MeV\)

Năng lượng tỏa ra là \(\Delta E = 2{K_X} - {K_p} = 14,6MeV\)

+ Năng lượng thu vào của phản ứng:  W_thu = K_α+ K_Al – (K_P + K_x)

+ Mà K_Al = 0, K_P = K_x  

=> K_P = K_x = 0,45 MeV

\(\begin{array}{l} \Rightarrow {v_P} = \sqrt {\dfrac{{2.{K_P}}}{{{m_P}}}}  = \sqrt {\dfrac{{2.0,45.1,{{6.10}^{ - 13}}}}{{30.1,{{66055.10}^{ - 27}}}}}  = 1,{7.10^6}m/s\\{v_X} = \sqrt {\dfrac{{2.{K_X}}}{{{m_X}}}}  = \sqrt {\dfrac{{2.0,45.1,{{6.10}^{ - 13}}}}{{1.1,{{66055.10}^{ - 27}}}}}  = 9,{3.10^6}m/s\end{array}\)

PT phản ứng: \(p + {}_4^9Be \to \alpha  + {}_3^6X\)

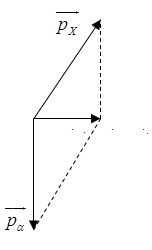
+ Theo định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_p}}  = \overrightarrow {{p_\alpha }}  + \overrightarrow {{p_X}} \)

=>  Ta biểu diễn bằng hình vẽ sau:

Từ hình vẽ ta có: \(p_X^2 = p_\alpha ^2 + p_p^2\)

Mà : \({p^2} = 2mK \Rightarrow {m_X}{K_X} = {m_\alpha }{K_\alpha } + {m_p}{K_p} \Rightarrow {K_X} = \dfrac{{{m_\alpha }{K_\alpha } + {m_p}{K_p}}}{{{m_X}}} = \dfrac{{4.4 + 1.5,45}}{6} = 3,575(MeV)\)

Phương trình phản ứng:  \({}_1^1p + {}_3^7Li \to {}_2^4\alpha  + {}_2^4\alpha \)

Năng lượng tỏa ra:  \(\Delta E = {K_s} - {K_t} = \left( {{K_\alpha } + {K_\alpha }} \right) - \left( {{K_p} + {K_{Li}}} \right) = 2{K_\alpha } - 1,6 = 17,4MeV \to {K_\alpha } = 9,5MeV\)

+ PT phản ứng: \(p + {}_4^9Be \to \alpha  + {}_3^6X\)

+ Theo định luật bảo toàn động lượng ta có: \(\overrightarrow {{p_p}}  = \overrightarrow {{p_\alpha }}  + \overrightarrow {{p_X}} \) 

=> ta biểu diễn bằng hình vẽ sau:

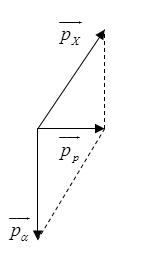
Từ hình vẽ ta có: \(p_X^2 = p_\alpha ^2 + p_p^2\)

Mà : \({p^2} = 2mK \Rightarrow {m_X}{K_X} = {m_\alpha }{K_\alpha } + {m_p}{K_p} \Rightarrow {K_X} = \dfrac{{{m_\alpha }{K_\alpha } + {m_p}{K_p}}}{{{m_X}}} = \dfrac{{4.4 + 1.5,45}}{6} = 3,575(MeV)\)

Năng lượng tỏa ra của phản ứng : \(\Delta E = {K_X} + {K_\alpha } - {K_p} = 3,575 + 4 - 5,45 = 2,125(MeV)\)

Phương trình phản ứng:  \(_6^{12}C \to _2^4He + _2^4He + _2^4He\)

- Năng lượng của bức xạ gamma: \(\varepsilon  = hf = 2,{65.10^{ - 12}}(J) = 16,5625(MeV)\)

- Theo định luật bảo toàn năng lượng toàn phần ta có:

\(\varepsilon  + {m_C}.{c^2} = 3\left( {{m_{He}}.{c^2} + {K_{He}}} \right) \Leftrightarrow \varepsilon  + {m_C}.{c^2} = 3{m_{He}}.{c^2} + 3{K_{He}}\)

=>  Động năng của mỗi hạt He là:

\({K_{He}} = \dfrac{{\varepsilon  + ({m_C} - 3{m_{He}}).{c^2}}}{3} = \dfrac{{16,5625 + (12 - 3.4,0015).931,5}}{3} = 4,124(MeV) \approx 6,{6.10^{ - 13}}(J)\)

Bảo toàn động lượng: \(\overrightarrow {{P_p}}  = \overrightarrow {{P_\alpha }}  + \overrightarrow {{P_\alpha }} \)

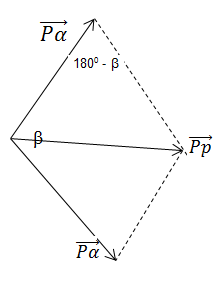
Năng lượng toả ra của phản ứng: \(\Delta E = 2{K_\alpha } - {K_p} \Leftrightarrow 17,3 = 2{K_\alpha } - 4,5 \Rightarrow {K_\alpha } = 10,9MeV\)

Áp dụng định lí hàm số cos trong tam giác:

\(\begin{array}{l}P_p^2 = P_\alpha ^2 + P_\alpha ^2 - 2{P_\alpha }{P_\alpha }c{\rm{os}}\left( {180 - \beta } \right) \Rightarrow P_p^2 = 2P_\alpha ^2\left( {1 - c{\rm{os}}\left( {180 - \beta } \right)} \right)\\ \Rightarrow {m_p}{K_p} = 2{m_\alpha }{K_\alpha }\left( {1 - c{\rm{os}}\left( {180 - \beta } \right)} \right) \Rightarrow c{\rm{os}}\left( {180 - \beta } \right) = 1 - \dfrac{{{m_p}{K_p}}}{{2{m_\alpha }{K_\alpha }}} = 1 - \dfrac{{1.4,5}}{{2.4.10,9}} = \dfrac{{827}}{{872}}\\ \Rightarrow 180 - \beta  = 18,{5^0} \Rightarrow \beta  = 161,{5^0}\end{array}\)

Phương trình phản ứng hạt nhân: \(p + {}_3^7Li \to {}_2^4X + {}_2^4X\)

Năng lượng toả ra của phản ứng: \(\Delta E = \left( {{m_p} + {m_{Li}} - 2{m_X}} \right){c^2} = 2{K_X} - {K_p} \Rightarrow {K_X} = 9,866MeV\)

Định luật bảo toàn động lượng: \(\overrightarrow {{P_p}}  = \overrightarrow {{P_X}}  + \overrightarrow {{P_X}} \)

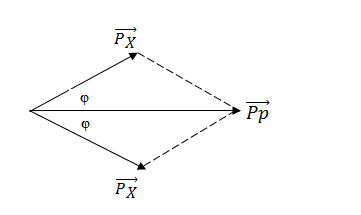
Áp dụng định lí hàm số cos trong tam giác ta được: \(P_X^2 = P_X^2 + P_p^2 - 2{P_X}{P_p}c{\rm{os}}\varphi \)

\( \Rightarrow \cos \varphi  = \frac{{p_p^2}}{{2{p_X}{p_p}}} = \frac{{{p_p}}}{{2{p_X}}} \Rightarrow {P_p} = 2{p_X}\cos \varphi \)  

\(\begin{array}{l} \Rightarrow p_p^2 = 4p_X^2{\cos ^2}\varphi  \Leftrightarrow {m_P}{K_P} = 4{m_X}{K_X}{\cos ^2}\varphi  \Rightarrow {\cos ^2}\varphi  = \dfrac{{{m_P}{K_P}}}{{4{m_X}{K_X}}} = \dfrac{{1.2,5}}{{4.4.9,866}}\\ \Rightarrow \varphi  = 82,{7^o}\end{array}\)

+ Phương trình phản ứng: \({}_0^1p + {}_4^9Be \to {}_2^4\alpha  + {}_2^6X\)  

+ Năng lượng toả ra của phản ứng hạt nhân: ∆E = K_α + K_X – K_p = 2,125

=> K_p = 4,6 MeV

+ Áp dụng định luật bảo toàn động lượng: \(\overrightarrow {{p_p}}  = \overrightarrow {{p_X}}  + \overrightarrow {{p_\alpha }} \)

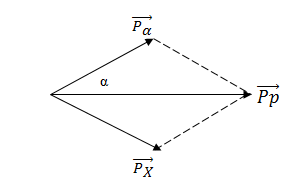
Áp dụng định lí hàm số cos ta có: \(p_X^2 = p_p^2 + p_\alpha ^2 - 2{p_p}{p_\alpha }c{\rm{os}}\alpha \)

\(\begin{array}{l}{p^2} = 2mK\\ \Rightarrow 2{m_X}{K_X} = 2{m_p}{K_p} + 2m{K_\alpha } - 4\sqrt {{m_p}{K_p}{m_a}{K_\alpha }} cos\alpha \\ \Leftrightarrow {m_X}{K_X} = {m_p}{K_p} + {m_\alpha }{K_\alpha } - 2\sqrt {{m_p}{K_p}{m_a}{K_\alpha }} cos\alpha \\ \Leftrightarrow 6.3,150 = 1.4,6 + 4.3,575 - 2\sqrt {1.4,6.4.3,575} cos\alpha \\ \Rightarrow cos\alpha  = 0\\ \Rightarrow \alpha  = {90^0}\end{array}\)

Khối lượng các hạt nhân phải đạt khối lượng tới hạn không phải là điều kiện xảy ra phản ứng nhiệt hạch.

Cách giải:

Năng lượng phản ứng toả ra là:

 \(\begin{array}{l}\Delta E = \left( {\sum {{m_{trc}}}  - \sum {{m_{sau}}} } \right){c^2} = \left( {{m_{Li}} + {m_H} - 2{m_{He}}} \right){c^2}\\\,\,\,\,\,\,\,\, = \left( {7,0144 + 1,0073 - 2.4,0015} \right).91,5 = 17,42MeV\end{array}\)

Năng lượng tỏa ra của 1 phản ứng là :

\(E=({{m}_{X}}-2\Delta {{m}_{D}}).{{c}^{2}}=(0,0083-2.0,0024).931=3,2585MeV\)

1g \({}_{1}^{2}D\) có số hạt nhân là: \(N=\frac{m}{A}.{{N}_{A}}=\frac{1}{2}{{.6,023.10}^{23}}={{3,0115.10}^{23}}\)

Mỗi phản ứng tổng hợp được 2 hạt nhân \({}_{1}^{2}D\)

Vậy khi tổng hợp được 1g\({}_{1}^{2}D\) thì năng lượng tỏa ra là :

\({{E}_{toa}}=\frac{\Delta E.N}{2}=\frac{{{3,2585.3,0115.10}^{23}}}{2}={{4,906.10}^{23}}MeV\)

Năng lượng tỏa ra trong phản ứng:

E = 931,5. (m₀ – m) = (4,0015 + 26,97345 – 29,97005 – 1,99867).931,5 = - 3,51MeV

Vậy phản ứng thu năng lượng bằng 3,51 MeV